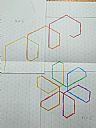
用ggb探討循環圖規律

專題名稱用ggb探討循環圖規律

專題描述 我們在百年哈佛給學生做的600個思維遊戲裡看到了一個引起我們興趣的題目：循環圖。於是我們就決定深入研究。
我們將n分成奇數和偶數來討論， 最後我們發現當n=6k，且k為大於0的整數時，畫出的循環圖是向左無限延伸，像一條線；當n=6k＋1，且k為大於0的整數時，是逆時針轉六個封閉圖；當n=6k＋2，且k為大於0的整數時，是逆時針轉三個封閉圈；當n=6k＋3，且k為大於0的整數時，是兩個封閉圈；當n=6k＋4，且k為大於0的整數時，是順時針轉三個封閉圈；當n=6k＋5，且k為大於0的整數時，是順時針轉六個封閉圖。
我們的研究是以三角形底紙每次轉彎逆時針旋轉60度來繪製，如果未來將底紙改成其他形狀，或調整旋轉的角度，也許有不同的結果和規律。

隊伍名稱薯條好好吃

指導老師謝孟琪　楊佳鳳

參賽學生陳冠妤　官品榛　　

序號檔案內容上傳者最後修改
3作者 不明
來源 屏東縣第 61 屆國中小學科學展覽會
描述 了解循環小數的意義、分數化為小數的種類、循環小數的特性以及如何將循環小數化為分數。		官品榛2025/9/24 下午 10:48:20
2作者 李信昌(昌爸)
來源 循環節對稱圖
描述 說明分數1/p的分母都是質數，而且1/p分別乘以 2、3、......、(p-1)，都還是循環小數，循環節是1/p循環節的旋轉排列。		官品榛2025/9/24 下午 10:00:51
1作者 曹緁軒、曹馨方、黃彥瑋、陳則智
來源 中華民國第 63 屆中小學科學展覽會
描述 利用Scratch 程式軟體將分數轉化成循環小數，並觀察其規律性，透過圖形反推循環小數		官品榛2025/9/24 下午 09:42:35

序號封面照內容說明上傳者最後修改
8類別 相簿集
名稱 原題
說明
右邊的循環圖表形每次轉彎時皆逆時針旋轉60度。圖中已畫出n=1、2、3和4時的圖形。你能畫出n=5、6、7和8時的圖形嗎？這是我們在《百年哈佛給學生做的600個思維遊戲》看到的題目，		陳冠妤2025/10/2 下午 09:30:44
7類別 相簿集
名稱 使用電腦
說明
在電腦教室一邊觀察用ggb畫的循環圖，一邊絞盡腦汁的想書面報告能打甚麼，並將想到的內容打到書面報告的檔案中，途中還因為圖片的順序問題多花了非常多的時間調整。		陳冠妤2025/10/2 下午 09:24:48
6類別 相簿集
名稱 手寫筆記
說明
這是我們在討論如果底紙圖形不一樣和旋轉角度不一樣會有甚麼規律。因此我們分別討論了1.底紙是正方形，轉90度2.底紙是正三角形，轉60度。我們發現：圖形底紙的邊的個數如果是6，那當n=6時，此循環圖就會無限延伸；當圖形底紙的邊的個數如果是4，當n=4時，此循環圖就會無限延伸；當圖形底紙的邊的個數如果是3，當n=3時，此循環圖就會無限延伸⋯⋯。		陳冠妤2025/10/2 下午 09:23:39
5類別 相簿集
名稱 使用電腦
說明
這是我們畫循環圖的過程。我們在畫圖的過程中，遇到了一個問題，那就是當我們把圖縮小時，圖紙的網格還是會維持原狀，所以我們畫的頂點就會變成不在底紙三角形的頂點上，後來我們發現，我們在畫之前，要將格線設定為「固定於格線」，就能解決問題。		陳冠妤2025/10/2 下午 09:08:58
4類別 相簿集
名稱 解原題
說明
我們依照題目在紙上畫出n=7和n=8的循環圖形，但是因為上次底紙上的三角形印得太大了，所以我們這次決定印小一點，結果又印的太小，且只有一小塊有底紙，我們只好又將多張紙拼起來，才夠將整個圖形畫出來，不過因為三角形印的比較小，最後的成品也比較小張。		陳冠妤2025/10/2 下午 09:05:18
3類別 相簿集
名稱 解原題
說明
我們依照題目在紙上畫出n=5和n=6的循環圖形，但是因為底紙上的三角形印得太大了，所以我們只好將多張紙拼起來，才夠將整個圖形畫出來。		官品榛2025/10/2 下午 09:03:13
2類別 相簿集
名稱 去圖書館
說明
在圖書館認真尋找和循環圖有關的書籍，但是和循環圖有相關的書籍非常少，所以我們還找了一些和數學有關的書籍，像是:學生必讀的100數學知識。		官品榛2025/10/2 下午 09:02:35
1類別 相簿集
名稱 使用電腦
說明
這是我們在使用ggb畫循環圖。我們一開始對ggb這個網站很不了解，不僅效率很低，還一直畫錯，尤其是當n的次數較高時，劃錯真的超崩潰！直到後來用久了，才發現一些節省時間的方法，例如：使用複製格式就不用一個一個的改顏色和隱藏物件還有標籤的部分也可以在一開始就設定隱藏。		陳冠妤2025/10/2 下午 08:50:28

序號內容上傳者最後修改
8作者 陳冠妤
標題 找文獻時的困擾
內容
在做小論文之前我們有查過相關的文獻，但是我們發現網路上相關的內容實在是少之又少！唯一能找到的就是維基百科上對循環圖的定義。 出現更多的是由好幾個箭頭連接成環形的圖。

陳冠妤2025/10/2 下午 10:21:19
7作者 陳冠妤
標題 製作書面報告時遇到的困難
內容
我們把各個循環圖畫好後，就開始著手製作書面報告。但是過程中也遇到了許多問題，例如：圖片太多沒辦法在10頁以內放下、字體大小不一、電腦格式不同做出來的表格長得不一樣⋯⋯等。

陳冠妤2025/10/2 下午 09:42:27
6作者 官品榛
標題 在圖書館找書時遇到的問題
內容
我們在圖書館認真尋找和循環圖有關的書籍時，發現和循環圖有關的書籍數量很少，所以我們還找了其他和循環圖相關的書籍，像是因數和倍數、還有其他和數學有關的書籍，找書時有一個問題是:和循環圖有關的部分通常不會是整本書，只有一部分的章節，但有些書的目錄寫得讓人沒法一眼看出它的內容，只能一頁一頁翻找看看有沒有相關的內容，很花時間。

官品榛2025/10/2 下午 09:39:51
5作者 官品榛
標題 解原題時遇到的問題
內容
我們在用紙畫解原題，也就是n=5、n=6、n=7、n=8時，遇到了許多問題，像是不小心將底紙上的三角形印得太大，一張紙都沒辦法將一個循環圖畫完，只能將多張紙拼起來。下一次決定將三角形印小一點，卻又不小心印錯，紙上只有一小塊有底紙，只好又將多張紙拼起來。不過因為三角形比較小，所以最後畫出來的成品也有比較小張。未來印東西時一定要看清楚，才不會要多花時間把紙拼起來。

官品榛2025/10/2 下午 09:22:33
4作者 陳冠妤
標題 遇到的問題
內容
我們分成奇數和偶數來畫，但畫到一個段落後我們發現兩邊的起始角度不同，經過我們的討論後決定把偶數的截圖轉向，但還是有一個問題:起始點的文字不能轉！後來我們發現轉向後的截圖可以加文字，角度的問題也就解決了。

陳冠妤2025/9/25 下午 08:40:58
3作者 陳冠妤
標題 使用ggb的困難
內容
我們剛開始在使用ggb繪畫時，在如何使用的方面研究的非常久，從如何畫出帶有箭頭的線，如何去掉線，兩端的點，到如何改顏色，去掉標籤，最後終於得心應手。

陳冠妤2025/9/22 下午 09:04:20
2作者 官品榛
標題 畫ggb時的失誤和發現
內容
我在用ggb畫循環圖時，不小心在其中一條線少畫了一格，結果畫完後才發現圖形大小怪怪的，後來又花時間一條線一條線檢查並更正。這次的錯誤讓我知道比起最後才一口氣檢查，不如畫一條就檢查一條，也讓我發現左邊的代數區能清楚看見線條的長度，就更不容易畫錯。

官品榛2025/9/19 下午 05:39:21
1作者 官品榛
標題 用ggb畫循環圖時的意外發現
內容
我們在ggb上畫循環圖時發現n=的數字越大，畫起來越花時間，且一個一個數格子很容易數錯，我們想知道有沒有更簡單的方法，於是我們觀察了畫好的循環圖，發現只要將兩條線的內角的中間向外延伸6格，再從上一條線的末端連到延伸出來的點，就能簡單畫好線。

官品榛2025/9/19 下午 05:20:00

序號封面簡介（摘要）上傳者最後修改
4書名 史上最強圖解．數學
作者 數學能力開發研究會
出版社 漢湘文化事業股份有限公司
簡介（摘要）
從加法算數、圖形、公因公倍數、函數與方程式、機率，多個從小學到高中的數學基礎概念都有詳細圖解，一看就會！皆可在日常生活中輕鬆活用。
導讀
全彩的圖解，將各種知識和公式做成圖解，非常內容詳細、配上圖能輕鬆了解概念。		官品榛2025/9/30 下午 12:57:50
3書名 小學六年幾何概念
作者 西村 則康/辻 義夫 陳識中
出版社 台灣東販股份有限公司
簡介（摘要）
本書由日本補教界名師編纂，針對整個小學六年幾何中最容易搞混的部分，配合圖解，提供了許多即使是小孩子也能看懂的解說。
導讀
書中有十分清楚的文字解說，配上可愛的插圖，讓人一看就懂。		陳冠妤2025/9/23 下午 01:06:47
2書名 學生必讀的100數學知識
作者 金英志 劉芸
出版社 企鵝國際出版股份有限公司
簡介（摘要）
數學是個需要理解，不是只靠死背的科目。為了培養學童的數學解題能力，不應過於重視答案是否正確，應該擁有「為什麼會得到這個答案？」的探討精神。
導讀
學生必讀的100數學知識這本書裡用淺顯易懂的文字和圖片來講解一些重要的觀念。		陳冠妤2025/9/23 下午 12:57:38
1書名 百年哈佛給學生做的600個思維遊戲
作者 黎娜
出版社 禾風車書版股份有限公司
簡介（摘要）
享受風靡國際的思維遊戲，有效訓練思考能力，迅速開發大腦潛能。
導讀
在「百年哈佛給學生做的600個思維遊戲」裡，有很多很有趣的數學題，每個都值得我們去討論。		陳冠妤2025/9/22 下午 10:00:47

序號截圖網站簡介上傳者最後修改
3網站名稱 倍數-教育百科
網址 https://pedia.cloud.edu.tw/Entry/WikiContent?title=%E5%80%8D%E6%95%B8&search=%E5%80%8D%E6%95%B8#.E5.8F.83.E8.80.83.E8.B3.87.E6.96.99
網站簡介
用簡單易懂且詳細的方式講解因數和倍數，解說最小公倍數的算法和一些求最小公倍數的程式寫法。		官品榛2025/9/23 下午 09:18:13
2網站名稱 數感實驗室
網址 https://numeracylab.com
網站簡介
數感實驗室是國內首屈一指生活數學教育品牌，臺師大第一家衍生教育新創企業。實驗室由臺師大副教授賴以威和妻子共同創辦，承接父親推廣趣味數學的遺志，強調「動手學數學」的實驗概念，並以舉辦數學實驗課和互動展覽等方式廣受歡迎。		陳冠妤2025/9/23 下午 08:53:05
1網站名稱 循環圖-維基百科
網址 https://zh.wikipedia.org/zh-tw/%E5%BE%AA%E7%8E%AF%E5%9B%BE
網站簡介
介紹循環圖的定義、屬性、術語和組成要素。及有向循環圖的定義和簡介		官品榛2025/9/20 下午 06:47:38

序號書面報告說明上傳者最後修改
1說明 我們在百年哈佛給學生做的600個思維遊戲裡看到了一個引起我們興趣的題目：循環圖。於是我們就決定深入研究。
我們將n分成奇數和偶數來討論， 最後我們發現當n=6k，且k為大於0的整數時，畫出的循環圖是向左無限延伸，像一條線；當n=6k＋1，且k為大於0的整數時，是逆時針轉六個封閉圖；當n=6k＋2，且k為大於0的整數時，是逆時針轉三個封閉圈；當n=6k＋3，且k為大於0的整數時，是兩個封閉圈；當n=6k＋4，且k為大於0的整數時，是順時針轉三個封閉圈；當n=6k＋5，且k為大於0的整數時，是順時針轉六個封閉圖。
我們的研究是以三角形底紙每次轉彎逆時針旋轉60度來繪製，如果未來將底紙改成其他形狀，或調整旋轉的角度，也許有不同的結果和規律。		謝孟琪2025/9/26 上午 10:45:21