探索小星星的邊角世界
| 專題名稱 | 探索小星星的邊角世界 |
| 專題描述 | 小時候學畫星星 , 最常畫的是五角或是六角的星星 , 於是我們聯想到 , 是否可以畫出七角、八角甚至更多角的星星 ? 若可 , 是否可以算出N角星的每個內角的度數、內角和度數、邊長各多少 ? 如果想利用圓規、直尺與量角器畫出邊長為a的N角星 , 那如何算出圓的外接圓半徑 ? 另外 , 不同的星星是否與世界各國的圖騰、國旗、歷史、文化有關連 ? |
| 隊伍名稱 | 戀戀慢城 |
| 指導老師 | 陳志彥 |
| 參賽學生 | 江芝其 楊昀臻 |
| 序號 | 檔案 | 內容 | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 5 |  | 作者 維基百科網站 來源 維基百科網站 描述 維基百科搜尋關鍵字「尺規作圖」結果 , 意外發現 , 原本在教科書上定義的尺規作圖是用不可有刻度的直尺與圓規 , 不過在維基百科網站上提到 , 也有部分的尺規作圖是可以利用刻度的 , 甚至可以利用量角器 , 因此本次研究正是利用有刻度的直尺與圓規及量角器進行繪製正多角星 | 陳志彥 | 2021/10/7 下午 08:05:17 |
| 4 | | 作者 維基百科網站 來源 維基百科網站 描述 從維基百科網站關鍵字搜尋「五角星」結果 , 針對五角星運用在人類歷史古文明及宗教上出現的文獻記載 | 陳志彥 | 2021/10/6 下午 04:04:07 |
| 3 |  | 作者 維基百科網站 來源 維基百科網站 描述 童年的記憶--正五角星與正六角星 , 因而聯想出是否能用直尺圓規與量角器做出更多角的星星(如 : 七角星、八角星、九角星.......等)，並欲找尋有關多角星星的相關文獻 , 透過維基百科網站搜尋 , 找尋到星星多邊形的許多國中課本找不到的數學文獻 | 陳志彥 | 2021/9/30 下午 07:00:39 |
| 2 | | 作者 維基百科網站 來源 維基百科網站 描述 本次研究因為需要在給定邊長的狀況下 , 計算正多角星之外接圓半徑 , 計算過程中必須使用到高中三角函數的基本概念與公式 , 因而引發我們對三角函數等相關歷史文獻的興趣 , 透過維基百克搜尋關鍵字 「三角函數」的介紹 , 找到許多就數學、歷史、文明、人文等多元面向與角度來看不一樣的三角函數 | 陳志彥 | 2021/9/30 下午 06:49:19 |
| 1 | | 作者 結城浩 來源 維基百科 描述 因本次研究須用到三角函數概念計算正多角星 , 因而找到此書 , 也引發對本書作者的興趣 , 為何有人有興趣把數學書寫得如此有趣 ? 甚至發表許多非常少見與數學有關的數學小說 , 因而引起本研究團隊對於本書作者的興趣 | 陳志彥 | 2021/9/30 下午 06:34:17 |
| 序號 | 封面照 | 內容說明 | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 8 |  | 類別 相簿集 名稱 利用三角函數概念計算正六角星外接圓半徑 說明 利用剛剛我們所研究出來的正五角星外接圓半徑求法 , 以同樣方法來嘗試計算正六角星的外接圓半徑 | 楊昀臻 | 2021/9/23 下午 01:38:17 |
| 7 |  | 類別 相簿集 名稱 利用三角函數概念計算正五角星外接圓半徑 說明 利用八年級下學期所學的內角與外角的概念 , 先計算出正五邊形每個外角和每個內角的度數 , 再利用高中三角函數概念計算正五角星外接圓半徑 | 江芝其 | 2021/9/23 下午 01:29:30 |
| 6 |  | 類別 相簿集 名稱 學習基本的三角函數概念 說明 本次研究因為需要用到高中三角函數觀念才能運算出正多角星的外接圓半徑 , 首先要學習且孰悉高中三角函數基本概念 | 江芝其 | 2021/9/23 下午 01:26:27 |
| 5 |  | 類別 相簿集 名稱 學校圖書室查關於正多角星的相關資料 說明 於鳳林國中圖書室查資料 , 找尋關於正多角星的種種相關記載 , 各種正多角星在人類歷史、古文明、宗教上又各代表何意義、運用與史蹟記載 | 江芝其 | 2021/9/10 下午 07:42:22 |
| 4 |  | 類別 相簿集 名稱 利用網路的三角函數計算機計算三角函數近似值 說明 利用網路的三角函數計算機計算非特殊角之三角函數近似值 , 進而求出正多角星在給定固定邊長時 , 其外接圓的半徑近似值 | 楊昀臻 | 2021/9/10 下午 07:38:13 |
| 3 |  | 類別 相簿集 名稱 上網路搜尋與討論關於正多角星的相關資料 說明 上網搜尋與討論正多角星的所有資料, 包含從數學、人文、歷史與宗教等不同角度與觀點之網路紀錄進行查詢 | 楊昀臻 | 2021/9/10 下午 07:35:56 |
| 2 |  | 類別 相簿集 名稱 正N角星每個內角及內角和求法研討 說明 1. 先求正N邊形的每個外角 2. 再求正N角星的每個內角 = 180-2×(正N邊形的每個外角) 3. 最後求正N邊形的外角和 = 正N角星的每個內角×N | 陳志彥 | 2021/8/30 下午 08:37:22 |
| 1 |  | 類別 相簿集 名稱 親手繪製多角星 說明 1. 學生親身體驗以尺規及量角器繪製五角星、六角星、七角星、八角星。 2. 以五角星為例 , 先用圓規以適當的長為半徑畫一圓 。 3. 將360除以5得到72度 , 再以量角器將圓周等分為5等份 , 每等份72度。 4. 再將等分點依序以直尺連接 , 繪製完成一個五角星。 5. 以此類推 , 再繪製出六角星、七角星、八角星。 | 陳志彥 | 2021/8/30 下午 08:30:51 |
| 序號 | 內容 | 上傳者 | 最後修改 |
|---|---|---|---|
| 6 | 作者 楊昀臻 標題 三角函數運用在正多角星計算及利用網路計算機求其近似值的神奇感受 內容 現在我們已經學到了正多邊星形的內角要怎麼算了，那我就更好奇了，如果我要畫出我想要的邊長呢？像是每邊一公分的正五角星。於是，我們又跑去找老師了，但老師居然說要運用的三角函數！ 老師舉例說，正五角星內部有正五邊形，五邊形的每個內角為108度，外角是72度，依此方法 , 可以計算出正五角星的每個銳內角度數 , 更令人興奮的是 , 因為要計算正五角星的外接圓半徑 , 所以不得不使用高中三角函數概念 , 能夠提前先修學到這個部分 , 更令我開心期待 , 神奇的是 , 在科技便利的現今 , 就算不使用三角函數查表 , 也能利用網路計算機計算出三角函數的近似值！ 在做這個的時候雖然有點累，但我覺得我很棒，因為不只可以複習功課，還可以預習數學！ | 楊昀臻 | 2021/10/6 上午 09:15:50 |
| 5 | 作者 江芝其 標題 高中三角函數初體驗 內容 剛開始在上三角函數的時候，覺得好難，因為是高中的課程，所以剛開始會有些吃力，一開始是要算「如果要讓五角星的邊長都是1的話，那圓的半徑要多少」，上課前我想說：「這不可能吧，太難了算不出來。」可是當老師將圖形分解一步一步帶著我們算的時候，發現好像還可以接受，不會太難而且消化得了，雖然說現在給我一個五角星要我算圓的半徑是多少的話，可能還不行，但是如果在熟悉那個公式和計算過程之後，可能就會在進階到六角星了 | 江芝其 | 2021/10/4 上午 09:31:04 |
| 4 | 作者 楊昀臻 標題 從數學中居然能學到歷史、人文，真讓人覺得驚訝 ! 內容 在決定做成小論文的當下，我們就馬上上網去查詢關於正多邊星形的一些事情，卻在這個時候我們發現到，星形居然和歷史有關係！ 舉例來說：五角星在基督教中代表著五種感官或基督的五種傷口，但現在大多代表異教徒及魔鬼撒旦；而在摩洛哥國旗上代表著神與摩洛哥國的聯繫。八角星是伊斯蘭的標誌，常常出現在信仰伊斯蘭文化的國家。十二角星則出現在諾魯的國旗上，代表著住在島上的十二的部落。 從數學中居然能學到歷史人文真讓人覺得驚訝。 | 楊昀臻 | 2021/9/22 下午 01:31:18 |
| 3 | 作者 江芝其 標題 數學居然與歷史、人文、宗教有很深的連結 , 太有趣了 ! 內容 在研究“星星”的過程中，突然有一個問題浮了出來，就是這些星星與人類文化的關聯性 ? 怎麼如何“出土”呢？於是我和昀臻分頭進行 , 我們上網查了維基百科，意外發現到我們研究的五角星、六角星、七角星、八角星、十角星乃至十二角星 , 在西方國家或是伊斯蘭教國家的歷史古文明都有出現過 , 甚至與宗教有關。在西方文化中，六芒星被稱為「达維狄之星」也被俗稱猶太星，是猶太教的象徵，而十二芒星是“正”與“善”的代表。更妙的是 , 很多國徽或是古文明都跟星星有關的 , 尤其是伊斯蘭教, 而世界上不分東西方 , 太多國家的國旗都出現星星了 , 連我們認為少見的正七角星(因為360無法被7整除 )都出現在某些國家的國旗中 , 為何是七角星 ? 當然是有遮些國家的典故與歷史意涵喔 ! 在了解這些之前，我覺得他只是一顆星星，沒有什麼特別的，但在研究的時候，各種問題慢慢的浮現出來，查了維基百科才發現原來星星有很多特別意義和歷史。 原來數學研究與人類文明甚至宗教有如此關連 , 真是太有趣了 ! | 江芝其 | 2021/8/30 下午 08:58:06 |
| 2 | 作者 楊昀臻 標題 生活中平凡的日常 ,卻成為我們有趣的研究主題 內容 在上課時，總是會以星星來標示重點，這時我突然在想：正方形每個角為90度，正三角形為60度，那星星呢？正五角星、正六角星甚至是正七角星呢？有沒有方法可以快速的算出來呢？於是我就跑去問老師了，碰巧遇到了另一位同學，就一起聽了。 老師說，正多邊形的外角和都是360度。舉正五邊形為例：360度／5＝72度，那正五角星的每個角就會是180－72＊2＝36！以此類推，正六角星的每個內角是60度，正七角星的每個內角是540／7度...... 我很感謝老師替我解惑，能將這個發現做成小論文，我很高興。 | 楊昀臻 | 2021/8/30 下午 08:45:51 |
| 1 | 作者 江芝其 標題 搞懂數學的規律性 ,不再死背 , 反而輕鬆 內容 從小到大畫的星星看似是一個簡單普通的插圖、標記或是重點，但是我們突發奇想“星星”是怎麼構成的，所以我們現在正在思考並且解出這個答案。為什麼五角星可以一筆完成呢？為什麼六角星要兩筆，而且是兩個正反三角形組成的呢？有什麼關聯或是規律嗎？ 為了求出星星的外接圓 , 我們只好透過上網、參考書籍或請教老師來學習高中三角函數其求解 , 剛開始摸索學習三角函數時覺得聽得懂、很簡單，但是後面開始變換之後，有那麼稍稍的小吃力，因為那個不是我們現在的範圍，已經超出了現在的知識量，但是呢理解了那個規律和算法之後，你會發現其實沒有那麼難，有的時候數學不用靠死背，搞懂它的規律就會變的很輕鬆。 | 江芝其 | 2021/8/30 下午 08:43:10 |
| 序號 | 封面 | 簡介（摘要） | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 6 |  | 書名 睡夢中學三角 作者 木棉 出版社 下文化出版社 簡介（摘要） 面對數學課本與講義裡的三角函數，你會不會覺得自己像被一群公式定理追著跑，卻不知道為什麼要跑？ 如果你有這種感覺，那麼《睡夢中，學三角》就是為你而寫的三角函數學習書。 這本書中有兩位主角：一位是愛打瞌睡的小平，他的數學老師叫做「老罩」（老是罩不住）；另一位是大M，是小平在睡夢中遇見的「數學守護神」。 透過小平與大M在睡夢中的對話，這本書會帶著你熟悉三角函數背後的運作邏輯，用靈活的方法及觀點來思考三角問題，幫助你擺脫「囫圇吞棗，拚命死背」的命運。 你希望自己從看到公式就頭大的苦命學生，蛻變成一流的數學高手嗎？ 閱讀這本書，這個改變也會發生在你的身上。 導讀 這本書的內容並不難，很適合高一下正要開始學三角函數的同學自修用。 大麥老師的建議是別把這本書當教科書看，與其說它是本三角函數的課本， 還不如說是一個已經讀過三角函數的工程師，以他學習的經驗，再一次去 理解三角函數。所以內容比較像「怎麼去學會」，而不是「教你什麼」。 如果早一點發現這本書，就會推薦給高一二的同學當作寒假催眠書呢！ 現在都快開學了，要催眠多得是課本，哪有時間再來看這種閒書呢？ 面對數學課本與講義裡的三角函數，你會不會覺得自己像被一群公式定理追著跑，卻不知道為什麼要跑？ 如果你有這種感覺，那麼《睡夢中，學三角》就是為你而寫的三角函數學習書。 這本書中有兩位主角：一位是愛打瞌睡的小平，他的數學老師叫做「老罩」（老是罩不住）；另一位是大M，是小平在睡夢中遇見的「數學守護神」。 透過小平與大M在睡夢中的對話，這本書會帶著你熟悉三角函數背後的運作邏輯，用靈活的方法及觀點來思考三角問題，幫助你擺脫「囫圇吞棗，拚命死背」的命運。 你希望自己從看到公式就頭大的苦命學生，蛻變成一流的數學高手嗎？ 閱讀這本書，這個改變也會發生在你的身上。 | 江芝其 | 2021/10/1 下午 01:34:00 |
| 5 |  | 書名 數學女孩秘密筆記：圓圓的三角函數篇 作者 作者： 結城浩 / 譯者： 陳朕疆 出版社 世茂出版社 簡介（摘要） 三角形與圓的關係，平面座標→向量→函數， 融會貫通，掌握脈絡！ 提問→算式→本質， 介紹「波利亞解題」，教你學習的方法！ 數學女孩再次帶你深入數學，由淺入深 高中數學的瓶頸，輕鬆突破！ 座標平面、圖形與向量，都是表示點的方法， 利薩如圖形(Lissajous) sin的記憶方法 函數、圖形、向量的關聯 求圓周率的概略值，助你了解三角函數！ 正九十六邊形的奧秘大公開！ 米爾迦、蒂蒂、由梨， 攜手波利亞、阿基米德， 變換圖形、把玩公式， 讓數學幻化成青春的蝶影， 教人不得不迷戀、追求！ 導讀 原本以為三角函數會非常艱深難懂 , 而且很無趣 , 看完這本書，發現作者極具巧思地用一群高中生的浪漫青春故事，結合詳細、有趣的數學辯論，講述費馬最後定理、哥德爾不完備定理、隨機演算法、伽羅瓦理論等主題。還發現廢瑪最後訂理居然跟畢氏定理有點像 , 如果不是這次參與小論文研究 , 也不會有機會先學習高中三角函數定理 , 更不會有機會閱讀有關數學的課外讀物是如此引人入勝 , 從這本書中發現 , 除了三角函數 , 也意外發現 : 正九十六邊形、螺旋、平面及空間向量、利薩如圖形(Lissajous)......等 也意外發現三角函數的最基本概念原本艱澀難懂 , 居然被作者介紹得非常有趣且淺顯易懂 , 甚至看完還想推薦對數學有興趣的同學鑽研。 那些原本在高中課本出現的難懂公式 , 也變得有趣容易理解 , 增加了我們對本次小論文研究的興趣 , 而數學女孩「秘密筆記」系列是作者集結網路上，讀者針對數學女孩系列提出的問題，整理成篇，以人物談話的方式，再次深入淺出地解說各數學概念。本書為「圓圓的三角函數」篇，集中討論讀者對三角函數的疑惑，貫通座標平面、向量、矩陣、螺旋等觀念，切中要點，詳細說明，延伸補充，讓讀者從各個角度認識三角函數，掌握圖形與公式，融會貫通，不用死背便能學好數學。 | 陳志彥 | 2021/9/30 下午 06:21:19 |
| 4 |  | 書名 翰林版高中數學【二上】課本 作者 翰林出版社高中數學教科書編輯團隊 出版社 翰林出版社 簡介（摘要） 本冊的高中數學教科書 , 主要介紹下列主題 : 1. 正弦、餘弦與正切 2. 廣義角定義 3. 度度量與弧度量的轉換 4. 廣義角的正弦、餘弦、正切 5. 直角坐標與極坐標的變換 6. 三角函數 : 正弦定理 7. 三角函數 : 餘弦定理 8. 三角函數 : 餘弦的和角與差角公式 9. 三角函數 : 正弦的和角與差角公式 10.三角函數 : 正切的和角與差角公式 11.三角函數 : 二倍角公式 12.三角函數 : 三倍角公式 13.三角函數 : 半角公式 14.三角函數值表 15.平面測量 16.立體測量 17.直線的斜率 18.直線方程式 19.兩線關係(垂直、平行、相交) 20.二元一次聯立方程組的解與其幾何意義 21.二元一次不等式 22.線性規劃的應用問題 23.圓的方程式 24.圓與直線的相切、相割、不相交的關係及其代數判定 25.有向線段與向量運算 26.向量的線性組合 27.平面向量的分點公式 28.三點共線定理 29.向量內積的定義 30.平面向量的正射影與高 31.平面向量與柯西不等式 32.平面上的直線參數式 33.平面上點到直線的距離 34.兩直線的夾角與角平分線 35.直線與圓的關係 36.二階行列式的定義 37.面積公式 38.二階克拉瑪公式 導讀 本次研究需要使用三角函數還計算正多角星再給定固定邊長 , 計算出其外接圓半徑 , 故須預先學習三角函數的基本概念 , 本次研究須要用到的基本觀念有 : 正弦定理、餘弦定理、餘弦的和角與差角公式、正弦的和角與差角公式、正切的和角與差角公式、二倍角公式、半角公式、三角函數值表。 | 陳志彥 | 2021/9/30 下午 06:11:57 |
| 3 |  | 書名 國中數學2下課本 作者 南一出版社編輯團隊 出版社 南一出版社 簡介（摘要） 國中數學八年級下學期教科書內容 , 主要是介紹「等差數列基本概念、等差級數(數列求和)、凸多邊形的的內角與外角、尺規作圖、三角形全等性質與證明、三角形的邊角關係、平行線、平行四邊形、特殊四邊形(鳶行、梯形、等腰梯形)」。 導讀 本次研究因為需要計算正多角星的每一個銳內角的度數 , 需要運用到多邊形的內角和與外角和 , 正多邊形的每個內角與外角度數之求法 , 才能解出。 | 江芝其 | 2021/9/30 下午 05:59:28 |
| 2 |  | 書名 Flying Colors國旗的故事：世界國旗的設計、歷史與文化 作者 Robin Jacobs / 譯者 : 蔡伊斐 出版社 麥浩斯 簡介（摘要） 這是一本關於世界上各種國旗的書，你可能在下面這些地方看過這些國旗：飄揚在宮殿的屋頂上、在重要的政府機關外排成長長的一列、國慶日時掛在路上、飄在帆船的桅杆頂端、畫在足球迷的臉上或是插在高級乳酪的小竹籤上…… 但是為什麼國旗看起來像這樣？ 導讀 原本是想研究且找尋有關正多角星在世界各國歷史文化之運用，沒想到在搜尋時意外發現多角星居然出現在很多國家的國旗中 , 輾轉找到這本書 , 例如 : 當我們正當愁著找不到很冷門的正七角星時 , 意外發現原來澳大利亞國旗有正七角星 , 而關於其介紹正是出自於「Flying Colors國旗的故事：世界國旗的設計、歷史與文化」這本書 , 而無論從這本書或是網路資料都發現 , 人類歷史上正多角星常出現與基督教與伊斯蘭教有關，然而有趣的是 , 我們從小熟悉象徵青天白日與戰士鮮血(三種顏色象徵自由、平等、博愛)的中華民國國旗中華民國國旗也出現「類似」正12角星 , 也就是青天白日 , 甚至我們認為一定是矩形的國旗 , 其實尼泊爾的國旗並不是四邊形 , 每個國家的國旗舉行的長寬比例也不盡相同 , 而波蘭、摩納哥和印尼的國旗幾乎一模一樣，都是紅白雙色旗 , 令人無法分辨 , 從沒想過這次研究 , 會讓從一向從不涉略研究世界各國國旗的我 , 因為找資料而看見國旗的有趣面貌 , 也是此次研究意外的驚喜與收穫 ! | 江芝其 | 2021/9/30 下午 05:52:40 |
| 1 |  | 書名 三角函數：三角函數的基礎入門書 少年伽利略2 作者 日本牛頓出版社編輯團隊/著 , 黃經良/譯 出版社 人人出版社 (日本牛頓出版獨家授權台灣人人出版社出版) 簡介（摘要） 正是由於三角函數可以在生活中驗證應用，所以對於數學學習特別重要。能愉快地學習三角函數，就比較可能跟數學發展出正向的關係。透過《三角函數：三角函數的基礎入門書》的豐富圖解，分章列點，突顯重點，讓讀者可以掌握脈絡，快速學習、有效學習。本書也整理了餘弦定理、正弦定理等重要公式，方便複習。 導讀 一、何謂三角函數？ 從三角形的性質衍生出的方便函數 二、首先來看看三角形吧 三角形是一切圖形的基礎 使用一根棍子測量金字塔的高度！ 紀元前就已求得地球一周的長度 古代測量所用的「3：4：5的直角三角形」 在直角三角形成立的「畢氏定理」是什麼？ 日本東京天空樹的視線所及範圍也能計算出來！ 利用三角形的性質製作出正確的地圖 Coffee Break 畢達哥拉斯趣味盎然的數學世界 三、三角函數的基本概念 從古希臘的天文學孕育出三角函數 第一個三角函數「正弦」 正弦的值在此時發揮作用！ 第二個三角函數「餘弦」 歷史上哪一個人物活用了餘弦？ 第三個三角函數「正切」 交通標誌上也應用了正切的值 四、三角函數彼此間的密切關係 正弦和餘弦是「表裡的關係」 「畢氏定理」把正弦和餘弦連結在一起 正弦、餘弦和正切可以連為一體！ 五、這麼方便！三角函數的重要公式 以cos為主角的「餘弦定理」是什麼？ 利用餘弦定理求算無法 直接測量的距離吧！ 以sin為主角的 「正弦定理」是什麼？ 在天文學中應用廣泛 的正弦定理 得知兩個角度之和或差之 三角函數的「和角公式」 Coffee Break 發現「和角公式」的托勒密 六、從三角形到「圓」 三角函數用「圓」來思考更容易理解！ 把三角函數從直角三角形的框架解放出來！ Coffee Break 角度可以用「圓弧的長度」來表示 七、從三角函數到「波」 把正弦的變化畫成圖形會變成「波」！ 餘弦的圖形也仍然是「波」！ 也來看看正切的圖形吧！ 「波」是什麼？ 「彈簧的振動」也隱藏著「波」 聲音、光、地震的搖晃⋯⋯，世界上充滿了「波」！ 八、支撐最尖端科技的三角函數 人聲、樂器的聲音也能用波形來表現 複雜的波其實是由單純的波「疊合」而成！ 分解複雜的波就可應用於數位機器上！ | 陳志彥 | 2021/8/11 上午 10:55:33 |
| 序號 | 截圖 | 網站簡介 | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 7 |  | 網站名稱 十二芒星有什麼意義 ? 百度知道 網址 https://zhidao.baidu.com/question/2075849393601876628.html 網站簡介 本網站針對根據中國古文引經據典、人類文明進程、數學、宗教等多元觀點來切入關於12芒星(正12角星) | 江芝其 | 2021/9/10 下午 07:59:10 |
| 6 |  | 網站名稱 澳洲聯邦之星---維基百科 網址 https://zh.wikipedia.org/wiki/%E6%BE%B3%E5%A4%A7%E5%88%A9%E4%BA%9E%E8%81%AF%E9%82%A6%E4%B9%8B%E6%98%9F 網站簡介 透過維基百科網站搜尋關鍵字"澳洲國旗" , 針對較為罕見的七角星 , 澳洲聯邦之星（英語：Commonwealth Star）是一個七角星圖案，為澳洲聯邦的象徵之一，自1901年1月1日開始使用。聯邦之星的六個角象徵澳洲原本的六個州，而第七個角則象徵澳洲未來的州分或領地。原本聯邦之星只有六個角，不過在1905年巴布亞領地劃入澳洲之後在1909年增加了第七個角[1]。聯邦之星也是澳洲國旗和圖案設計極為相似的紐西蘭國旗的主要不同之處。 | 楊昀臻 | 2021/9/1 下午 08:06:46 |
| 5 |  | 網站名稱 八角星---維基百科 網址 https://zh.wikipedia.org/wiki/%E5%85%AB%E8%A7%92%E6%98%9F 網站簡介 維基百科網站 , 針對八角星就數學、古文明、宗教(伊斯蘭文化)等多元角度與觀點來探討其關係 | 江芝其 | 2021/9/1 下午 07:56:08 |
| 4 |  | 網站名稱 六角星---維基百科 網址 https://zh.wikipedia.org/wiki/%E5%85%AD%E8%A7%92%E6%98%9F 網站簡介 維基百科網站針對六角星的部分 , 就數學、歷史、人文、宗教等多元角度與典故探討 | 楊昀臻 | 2021/9/1 下午 07:46:13 |
| 3 |  | 網站名稱 五角星---維基百科 網址 https://zh.wikipedia.org/wiki/%E4%BA%94%E8%A7%92%E6%98%9F 網站簡介 維基百科網站針對關鍵字"五角星"，就數學、歷史、人文、宗教、美學等不同角度與面向做介紹 | 陳志彥 | 2021/8/30 下午 09:05:18 |
| 2 |  | 網站名稱 十二芒星有什麼意義 ? 百度知道 網址 https://zhidao.baidu.com/question/2075849393601876628.html 網站簡介 介紹12芒星的意義 | 陳志彥 | 2021/8/29 下午 12:27:25 |
| 1 | 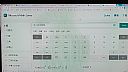 | 網站名稱 三角函數計算機 網址 https://mathsolver.microsoft.com/zh-Hant/trigonometry-calculator 網站簡介 本次研究需要求三角函數值 , 使用本網站之三角函數計算機可求其近似值 | 陳志彥 | 2021/8/29 下午 12:23:18 |
| 序號 | 書面報告 | 說明 | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 1 |  | 說明 探索小星星的邊角世界 , 藉由參閱網路文獻及國中、高中數學科教科書 , 運用正多邊形內角與外角觀念、三角函數基本概念 , 計算固定邊長的正多角星 , 其每個銳內角度數 , 及其外接圓半徑 , 而可以尺(有刻度的直尺)、圓規及量角器繪製出給定邊長的正多角星 , 並查閱網路及圖書資料 , 搜尋關於正多角星在人類歷史古文明、宗教、旗幟的運用情形。 | 陳志彥 | 2021/10/6 上午 09:09:34 |