同形同螺？
| 專題名稱 | 同形同螺？ |
| 專題描述 | 延伸第61屆數學科展「同形同螺」的作品，當時我們研究發現正ｎ邊形在等比例內縮與固定距離內縮的形況下，隨著內縮距離越來越小，多層正多邊形頂點連線所建構出來的螺旋線會越來越接近 「等角螺線」，因此取名為同形同螺，即同樣的形狀下不同內縮方式卻建構出一樣的螺線。而在這個作品中，我們想要做更多的延伸，以相同正多邊形為前提下，是否可以藉由別種排列方式來找出其他種類的螺旋線？這是我們想要研究的主題，因此在名稱上加一個問號。 |
| 隊伍名稱 | 螺旋考古隊 |
| 指導老師 | 潘恩勤 |
| 參賽學生 | 沈忻穎 王宜澄 黃彗紜 陳品妤 |
| 序號 | 檔案 | 內容 | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 10 |  | 作者 沈忻穎、陳志宇、廖翌辰 來源 電腦資料夾 描述 本研究探討正多邊形經特定的內縮方式而作出多層內切正多邊形後，其分割出圖形間之 邊長、面積、角度等關係，以及找出每層正多邊形對應頂點連接後所形成的軌跡與等角 螺線之間的關聯性。而圖形間的探討主要以 GeoGebra 數學線上繪圖軟體及試算表繪製出 各種正多邊形的內縮圖形並利用其式算表驗算我們所推導出的算式。 | 黃彗紜 | 2021/10/4 下午 05:29:50 |
| 9 | | 作者 谷超豪 來源 http://www.mathsgreat.com/curve/curve_indiv_025.pdf 描述 螺線 Spiral 是一系列曲線的統稱,凡圍繞一定點或軸轉動,同時又逐漸遠離定點之動點的軌跡,都可以稱為螺線。常見的平面螺線有阿基米德螺線、對數螺線、雙曲螺線、連鎖螺線、科努螺線等。 常見的空間螺線有圓柱螺線、一般螺線、彈簧、螺釘、螺旋樓梯等。 | 黃彗紜 | 2021/10/4 下午 05:28:14 |
| 8 | | 作者 邱渝萍、賈千躍、洪意淨 來源 https://www.ntsec.edu.tw/Science-Content.aspx?cat=&a=0&fld=&key=&isd=1&icop=10&p=290&sid=10129&fbcli 描述 本研究在探討A. Einstein所提出的三角形鋪砌凸多邊形問題：＂分別用1,2,3,...,N個從1開始的整數邊正三角形鋪砌一凸多邊形。問：怎樣鋪砌所構成的凸多邊形面積為最大？＂我們藉由觀察鋪砌正三角形的點、線、面關係發現以下幾點：一、鋪砌出的凸多邊形之頂點數(V)、邊數(E)、面數(F)具有V-E+F=1的性質，而當所鋪砌的圖形為一凹多邊形時，則其性質變成V-E+F=2。二、當N≥4時，最大面積凸多邊形必為五邊形。三、所鋪砌出的最大面積凸多邊形，其正三角形的邊長具有類似費氏數列的規律。 1,1,1,2,2,3,4,5,7,9,12,16,21,28,37,... 四、由黃金比例的探討發現，邊長數列雖也可繪製出類似鸚鵡螺曲線，但其曲線的半徑比卻無黃金比例的性質。五、後項與前項的比值趨近1.333，若用隔一項的比則會趨近於1.75。用最大正三角形的邊長與高的比則趨近1.539。 | 黃彗紜 | 2021/10/2 下午 04:26:57 |
| 7 | | 作者 王仁韋、李政興、蘇航、潘昱呈 來源 https://www.ntsec.edu.tw/Science-Content.aspx?a=6821&fld=&key=&isd=1&icop=10&p=1&sid=5074 描述 利用生物的幾何性質，歸納出生物成長的特殊規律性與數學幾何的密切關係。再針對菊科類植物花盤內螺旋線數量的獨特性質，去探討並推論其順、逆螺旋線數和費氏數列( Fibonacci Sequence ) 以及盧卡斯數列 ( Lucas Sequence ) 的特殊相關性，及其形成此規律性的原因。並藉由Maple執行各種不同發散角所模擬的花苞生長情形，來解釋為何黃金角是造成花苞排列緊密的最佳發散角。 | 黃彗紜 | 2021/9/29 下午 01:08:39 |
| 6 | | 作者 林漢維、吳岱潔、張育豪、蔡明翰 來源 https://www.ntsec.edu.tw/Science-Content.aspx?a=6821&fld=&key=&isd=1&icop=10&p=1&sid=404 描述 暑假時我們幾個同學想研究一些數學課外讀物，就向老師請教，老師建議我們去做比較有意義的學習，如製作科展，並提供一個方向-費氏數列，告訴我們:九大行星的距離、鸚鵡螺的螺旋角度，都和費氏數列有著微妙的關係呢!鼓勵我們費氏數列是一個大寶藏，只要花心思，很少會空手而回。於是開始展開我們研究的系列，蒐集往年的科展資料，上網路查詢，到師大數學系圖書館翻閱雜誌，到書局翻書找靈感.....，開始研究這一串神奇的數列。 | 黃彗紜 | 2021/9/29 下午 01:05:50 |
| 5 | | 作者 萬昇、周宗德、陳郁 來源 https://www.ntsec.edu.tw/Science-Content.aspx?a=6821&fld=&key=&isd=1&icop=10&p=1&sid=5157 描述 「非對稱性螺旋槳定理」是一個很有趣的定理，並且有好幾個相類似的推廣性質。我們 試著自己提出這些性質的證明，並且嘗試作一些推廣的探討。 | 黃彗紜 | 2021/9/29 下午 01:03:52 |
| 4 | | 作者 許翰翔 來源 https://www.ntsec.edu.tw/Science-Content.aspx?a=6821&fld=&key=&isd=1&icop=10&p=1&sid=10124 描述 此作品中，主要是研究「拿破崙定理」在四邊形條件下的各種推廣，將拿破崙定理在三角形條件下發現的各種規律類推到各種四邊形，並發現了許多有趣的結果。我的研究內容主要包含和拿破崙定理相近之重心連線；在其圖形中稍加變化而得的外接圓交點性質、面積性質；結合螺旋槳定理、愛可爾斯定理探討的頂點連線中點性質、和意外發現的共點性質。其中甚至有發現適用於任意四邊形的一般性質。目前在我找到的資料中，對於四邊形的討論著墨極少，大部分的文獻內容都針對三角形的性質做討論。 | 黃彗紜 | 2021/9/29 下午 01:00:49 |
| 3 | | 作者 林羿旻、林楷欣、林聖恩 來源 https://twsf.ntsec.gov.tw/activity/race-1/51/pdf/040421.pdf?fbclid=IwAR0urFcMmZk1YkQC4EJcypdmFyf2N0P 描述 仿照向日葵花盤生長的模式，我們單純的以數學方法：改變發散角φ，研究原基排列的 規則，有以下研究目的。 一、發散角與螺旋結構之關係 二、發散角產生雙螺旋結構的特性 三、發散角為 2π 的有理倍數亦產生雙螺旋結構 四、螺旋數目為 Lucas 數列相鄰兩項的向日葵的發散角與性質 | 黃彗紜 | 2021/9/29 下午 12:57:17 |
| 2 | | 作者 王聖文 來源 https://www.ntsec.edu.tw/Science-Content.aspx?cat=31&a=6821&fld=&key=&isd=1&icop=10&p=1&sid=4345&fbc 描述 小時候常常去海邊撿貝殼，那時我總是被貝殼上特殊的紋路深探地吸引著。上了高中無意問發現貝殼上的紋路很接近對數螺線的形狀，並且在科學月刊上看到趙文敏教授的文章，引起了我的興趣，可是在文中黃金螺線的部分並役有詳細的證明，於是我便探入地研究，在翡波那契數列那本書中看到了部分證明，我試圖補全所有的證明，經過多次的試驗，我意外發現黃金矩形所引出的螺線，一般書上的圖形並不嚴謹，這個發現讓我下定決心好好地研究對數螺線的性質及其推廣圖形。 | 黃彗紜 | 2021/9/29 下午 12:55:43 |
| 1 | | 作者 蘇熠治、陳柏諺 來源 https://twsf.ntsec.gov.tw/activity/race-1/59/pdf/NPHSF2019-030407.pdf 描述 本研究採用解析幾何方法發現，由正 n 邊形的特殊切割，發現了新正 n 邊形面積或與原正 n 邊形的面積比值都與切掉的小等腰三角形腰長或小正 n 邊形邊長具有特殊的二次函數的 關係。 | 黃彗紜 | 2021/9/29 下午 12:47:12 |
| 序號 | 封面照 | 內容說明 | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 10 |  | 類別 相簿集 名稱 10/6 最後衝刺 說明 老師打算今天就把全部都做好，真的很緊張，大家都在努力的打，不管是報告內容還是其他的，都在努力的趕，雖然會遇到不會的地方，但是大家還是努力詢問老師，一起加油 ，最後終於殺青成功。 | 陳品妤 | 2021/10/6 下午 06:40:45 |
| 9 |  | 類別 相簿集 名稱 10/4來用電子產品書寫 說明 今天中午我們到導師辦公室用電腦來把我們手寫的正多邊形螺旋的關係打到電腦上面，打的速度比想像中的快許多，多虧了分工合作所以我們快速的打了上去，再重新讀一遍，修改掉不順的地方，只花了午休就把它打完了。 | 陳品妤 | 2021/10/6 下午 01:11:22 |
| 8 |  | 類別 相簿集 名稱 10/2修正小論文中圖形的說明 說明 這天我們利用星期六下午的時間到校繼續撰寫小論文，我們主要來寫活動集，以及報告內容和正多邊形螺旋說明，在寫正多邊形螺旋說明的時候，遇到了重重困難，像是沒辦法解釋為什麼或是他們有什麼關聯，於是我們上網搜尋、詢問老師、查詢書籍，最後寫出正多邊形螺旋它的畫法以及關係。 | 陳品妤 | 2021/10/6 下午 01:11:16 |
| 7 |  | 類別 相簿集 名稱 10/1互相確認圖形規則的說明 說明 這天放學我們到了導師辦公室了解彼此的圖形規則說明，其中有些部分較難理解，所以我們互相討論，並把不適當的句子挑出來改掉，接著我們各自修改，再把修改好的打到電腦上面。但其實有些東西在當下會有些不明白，但後來聽老師和同學講解過後就清楚許多，其中我覺得固定頂點逆時針外擴最難寫/理解，因為關係比較複雜。 | 陳品妤 | 2021/10/6 下午 01:09:12 |
| 6 |  | 類別 相簿集 名稱 統整手繪正多邊形螺旋 說明 我把之前畫過的正多邊形螺旋手稿都統整過來拍照，其中我發現這些正多邊形螺旋都非常的美，看上去十分順眼，其中我們有畫了 1. 固定長度內縮的正多邊形螺旋-構思者沈忻穎 2.對應邊逆時針內縮的正多邊形螺旋-構思者黃彗紜 3.固定頂點逆時針外擴的正多邊形螺旋-構思者陳品妤 4.延著邊長外擴排列的正多邊形螺旋-構思者王宜澄 老師原本只教了我們用尺規作圖畫出正三角形，接著我們再慢慢延伸出上述四種正三角形螺旋形式。 | 陳品妤 | 2021/10/5 下午 01:18:12 |
| 5 |  | 類別 相簿集 名稱 9/30寫正三角形螺旋說明 說明 我觀察了其他人的書寫過程，我發現要用文字表達出來真的不簡單，他們首先先標示出點的名稱，接著觀察了正三角形螺旋的關係，再來一起討論後各自寫出來，寫的過程中也遇到許多瓶頸，不知道該如何表達、不知道他們的關係，於是他們上網搜尋，找出正三角形螺旋的關係，接著以簡單明瞭的方式書寫出來。 | 陳品妤 | 2021/10/4 下午 01:11:36 |
| 4 |  | 類別 相簿集 名稱 9/25去圖書館找書 說明 今天我們去學校圖書館找有關於螺旋以及幾何形的書，首先我們從名字以及圖片有相關的開始尋找，其中我們有找到一些有關的書，有找了《假麥田圈才是科學》、《幾何學用調查研究的方法探索》、《從正五邊形發起》、《生活的數學》等等的書，但是因為裡面相關的東西較少，所以我們只參考了《幾何學用調查研究的方法探索》和《這才是數學》這兩本書，我們原本有想要找纏繞畫以及貝殼圖鑑的書，但是因為學校圖書館的書比較少，所以我們希望學校的圖書館可以多買一些書，以及按照種類排序。 | 陳品妤 | 2021/9/28 下午 05:28:09 |
| 3 |  | 類別 相簿集 名稱 9/25用GGB畫出螺旋 說明 今天我們到了學校使用電腦用GGB畫出我們的螺旋圖案，照片中是我們三個人各自畫出來的作品。利用GGB我們可以延伸出更多的正多邊形螺旋圖案（一開始手繪只有探討正三角形螺旋），藉由電腦軟體我們可以更輕鬆的畫出其他的正多邊形的螺旋圖案，甚至標註顏色 | 陳品妤 | 2021/9/28 下午 01:21:35 |
| 2 |  | 類別 相簿集 名稱 9/16去電腦教室寫札記 說明 今天我們去電腦教室寫札記，我們記錄了我們這幾天學到和做的事情，幸好平時都有在上面寫日期，所以才能記得當天是畫哪張圖。 | 陳品妤 | 2021/9/25 下午 03:28:39 |
| 1 |  | 類別 相簿集 名稱 初次了解正三角形的畫法 說明 9/9號今天老師教我們畫正三角形和正六邊形，我們使用了尺和圓規來作畫。 我們先用尺畫出一條直線，接著在線上畫出一段距離，在兩端用圓規畫出兩個圓，圓的直徑要和你要的那段距離等長，再來在圓與圓之間的交會處畫出一條直線，再把三個點連起來，你就可以得到一個正三角形了，我們還可以利用正三角形畫出正六邊形。另外我們還繼續延伸，畫出多層正三角形外擴的螺旋式排列（每層正三角形的邊長以1/2倍遞減），因而找出新的螺旋線。 | 陳品妤 | 2021/9/24 下午 05:10:19 |
| 序號 | 內容 | 上傳者 | 最後修改 |
|---|---|---|---|
| 10 | 作者 沈忻穎 標題 總結心得 內容 從一開始的科展題目衍生到小論文；等比例內縮與固定內縮之間的邊長、面積、夾角關係討論到在小論文與其他夥伴、老師的集思廣益下，找到其他的圖形排列方式、螺線等討論。在這段期間，我也學到了很多。因為夥伴與科展時的不同，所以要再以一個新的方式去認識「同形同螺」。經由我們花了一個月的並將它改頭換面。加入了各種我們小論文的研究成果，我從沒想過這個題目可以衍生出這麼多的東西。也許下一次我們可以朝圖騰的研究方向再次出發。 | 沈忻穎 | 2021/10/7 下午 01:12:50 |
| 9 | 作者 黃彗紜 標題 從零開始的小論文 內容 一開始決定要做「同行同螺」這個主題時，感到擔心的同時也很興奮、期待，因為看起來很困難，害怕我們做不出一個好的成果，但又很激動可以用做小論文的名義來了解這些以前不曾遇到的問題、圖形。 在第一天時，我們學習到如何利用尺規畫出正三角形及垂直平分線的畫法，那時對於一切都還不太熟悉，動作都很生疏，但也是為這段時間的成果所打下的基礎（邁出第一步）。有了第一步後我們就各自畫出自己心中所想的螺旋。 過了幾天老師讓我們把自己畫的螺旋以文字具體的描述出來，我認為這是我們所遇到的第一個大難關，不過人生沒有過不去的坎，所以在卡了好一段時間後我們依舊解決了這個問題。 假日時我們利用ggb練習畫出前幾天所繪製的螺旋、雖然有點複雜，但現在讓我們來做已經駕輕就熟了！ 回想至九月初，再回到現在，雖然時間不長，但回憶著這一路我們所付出的時間、努力及我們所收穫的，讓我覺得好感動、也很開心能學到這麼多。 | 黃彗紜 | 2021/10/6 下午 05:53:58 |
| 8 | 作者 黃彗紜 標題 練習使用GGB 內容 9/25我們來到學校後先去圖書館尋找有關數學幾何、螺旋等相關的書籍，在找書的過程遇到了一些困難，幾乎都找不到有關的書，令我感到非常的煩躁，因為找到可以參考的資料很少。 後來到了電腦教室，我們把前幾天尺規所畫的正三角形螺旋圖以數學線上軟體GGB呈現出來，一開始會連錯點，也會畫錯方向讓圖形變得不一樣、沒有規律。雖然有點複雜，但在不斷的嘗試下我們已經開始慢慢掌握到一些技巧了，最後看到畫出來的成品內心成就感滿滿。 | 黃彗紜 | 2021/9/28 下午 05:42:46 |
| 7 | 作者 沈忻穎 標題 再次整理資料與重新認識 內容 我再一次地把之前科展所做的東西重新壓縮，留下等比例內縮及固定內縮這兩種內縮方式還有等角螺旋的介紹和定義以及所謂的黃金螺線，將他們寫進小論文中。 這段時間同學有找新的排列規則和螺線線，我也重新認識到了各種不同的排列方式而形成的各種螺線，像是沿著正三角形的對應邊向外排列。或是以正三角形的其中一個頂點為固定點，畫出多層正三角形移動形成不同的螺線等等，我覺得非常有意思。 | 沈忻穎 | 2021/9/28 下午 01:31:11 |
| 6 | 作者 陳品妤 標題 利用GGB把螺旋畫出來 內容 9/25我們到學校學習用GGB把我們的螺旋畫出來，以及到圖書館尋找相關書籍。 一開始老師先教我們如何使用GGB畫出圖來，接著我們開始嘗試畫出我們要畫的螺旋，先使用正多邊形這個功能畫出兩點你要的距離，再來打出你要的邊數，你就會得到一個你要的正多邊形，接著使用中心點在你要延伸出去的那個邊上，找出它中間的那個點，畫出另一個小正多邊形，依此類推繼續延伸，接著再把點跟點連起來，你就會得到一個螺旋。 | 陳品妤 | 2021/9/28 下午 01:15:08 |
| 5 | 作者 王宜澄 標題 利用ggb畫圖的心得 內容 9/25今天老師教我們使用ggb畫一些螺旋作品，其中老師教了我數列正三角形螺旋的畫法，竟然沒想像中的那麼難，過程也覺得相當有趣，像發現了新世界一樣。做完時非常有成就感，它的畫法是先畫一個起始邊長為1的正三角形，接著沿著其中一邊往外畫，則這個圖形由小到大、不斷纏繞的多層正三角形，我們得到了一個數列：1、1、1、2、2、3、4、5、7、9、12、16.........，我們發現這些數列有一定的規律，目前還在了解中。 | 王宜澄 | 2021/9/28 下午 01:06:43 |
| 4 | 作者 黃彗紜 標題 關於我們變成為螺旋小隊的這檔事 內容 9/10 學習利用直尺和圓規畫出正三角形、正方形、正六邊形，但是還不太熟悉所以動作很慢，還一直畫錯。 9/13 畫了一個由四個正三角形組成的螺旋，雖然一開始看不出圖形中的螺旋線，但在老師跟同學的討論之下發現我畫的圖裡面存在螺旋線，我非常激動我也可以找出螺旋線，同時也加深了我對正三角形螺旋圖形畫法的印象。 9/14 開始研究新螺旋的畫法，在經過多種嘗試之下，我又畫出不一樣的螺旋了.感覺自己好像進步了一些 9/15 老師請我們把這幾天畫的螺旋用文字描述出來，並寫在紙上，寫出來好像比畫出來困難很多，因為要把一個很抽象的圖形轉成具體的文字敘述，這件事情讓我的腦袋打結，久久生不出下一句。 | 黃慧紜 | 2021/9/16 下午 05:43:44 |
| 3 | 作者 王宜澄 標題 正六邊形螺旋探討 內容 9/10我們學會了利用直尺和圓規畫出正六邊形、三角形以及垂直平分線 9/13多次練習了正六邊形、三角形以及垂直平分線的畫法 9/14思考如何用正三角形和正六邊形排出不同的螺旋，並做出一件螺旋作品 9/15老師要我們用文字敘述9/14的作品，在寫的過程中，發現用文字敘述自己的作品是一件很困難的事情，很難清楚表達圖形的變化 我的作品說明如下: 畫出相同邊長的正六邊形，第二層以固定邊長內縮0.5公分的方式畫出，重複此步驟，會發現第一層內縮的長度會與第二層內縮的長度相同，並且能看到螺旋的形狀出現。 | 王宜澄 | 2021/9/16 下午 05:27:14 |
| 2 | 作者 陳品妤 標題 正三角形的螺旋探討 內容 9/10號學了正三角形與正六邊形以及正方形的畫法。 9/13號我們畫出了新的正三角形螺旋，我的作品是先畫了一個正三角形，固定其中一個點為中心， 選擇一邊再畫一個邊長縮小1/2倍的正三角形，再以同一個點為中心，在對應小正三角形的邊， 再畫一個邊長縮小1/4倍的正三角形，一直重複以上動作，就可以得到一個螺旋。 9/14號我繼續研究有沒有新的方法可以畫出螺旋，後來我嘗試用正六邊形畫出螺旋，但是我並沒有畫出來， 改天我打算再次嘗試，看能不能畫出新的螺旋。 9/15號老師要我們用文字表達我們畫出來的東西，頓時發現要用文字精確表達也是挺困難的。 | 陳品妤 | 2021/9/16 下午 04:59:42 |
| 1 | 作者 沈忻穎 標題 重新整理科展的資料 內容 我們將之前的科展資料重新整理，把原本26頁的研究過程刪減成6頁， 一開始先把重點用螢光筆畫出來並簡要改寫說明，再利用Word進行刪減修改留下我們需要的6頁內容，因為離科展有些時間了，某些細節都忘了，所以在修改時會抓不到重點，有時候會刪過頭，就要在開一個新檔很麻煩。 | 沈忻穎 | 2021/9/16 下午 04:47:31 |
| 序號 | 封面 | 簡介（摘要） | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 10 |  | 書名 樂活享繪禪繞畫：只要一支筆，就能快樂繪畫 作者 蕭淑玲 出版社 旗林文化 簡介（摘要） 真的很簡單，只要一支筆，就能輕鬆畫畫！ 不分年齡層，從幼童到長者都能輕易入門。 透過重複繪製相同圖案，進入專注且放鬆的狀態，讓內心得到平靜。禪繞畫由美國芮克‧羅伯茲與瑪莉亞‧湯瑪斯夫妻創造這種具有心靈療癒力的創作藝術。因為禪繞畫不需要草稿，只要一支筆、一張紙，再運用簡單的點、線、弧、曲、圈，重覆基本的圖形，創作出美麗的圖畫，並在規律且一筆一畫構成圖樣的過程中，讓自己進入專注的狀態，且從中得到心靈的平靜。 導讀 這本書裡有很多漂亮的纏繞圖，其中維特魯特的畫法是先畫一個圓，在圓裡在畫一個內接正方形，在往內接續畫一個圓，以及圓內接正方形，層層往內畫，就變成一朵漂亮的玫瑰花，再多畫幾個就可以達到一束玫瑰花，這個畫法只是基本型，其中還有延伸繪畫，就是在一堆花的周圍加上一些線條，形成螺旋，我覺得這些幾何圖形跟我們的研究內容很相似，值得參考！ | 陳品妤 | 2021/10/7 下午 05:41:25 |
| 9 |  | 書名 摺紙幾何學 作者 前川淳 翻譯﹔陳朕疆 出版社 世茂出版 簡介（摘要） 摺紙×幾何學 享譽全球的摺紙數學 世界摺紙粉絲引頸期盼的經典作品集中文版！ 以『前川定理』、『剛性摺疊』聞名世界的日本摺紙大師前川淳， 代表作品『惡魔』號稱眾人爭相模仿的摺紙界最強創作。 大師的第一本中文版作品集，摺紙迷怎麼能錯過！ 杜勒多面體、神明鳥居、大衛之星…收錄60種特殊摺紙作品， 教你折近年摺紙界主流的組合式摺紙！ 導讀 我們發現摺紙中的摺痕、折法也有產生不同的螺旋效果例如﹔立方辦八面體它所呈現的螺旋式由中心向外擴散。小十二二面半十二面體、正六邊形斷面立方體也有類似的排列方式，值得深入研究。 | 沈忻穎 | 2021/10/7 下午 05:37:11 |
| 8 |  | 書名 實用編籐工藝 作者 鄒柔華 出版社 美勞教育 簡介（摘要） 本書可算是”快樂籐編遊戲”的續篇，如果你學過基本的圓形編籃，本書剛好適合你進一步的學習編更美麗的作品。 如果你對手藝蠻有興趣，從本書開始學起也無妨，本書程度尚屬中等，不會太難的。 籐製品討人喜歡，自己動手編些器即學，即學即用更是有意思！ 導讀 我發現書內某些編織成品似乎藏有螺旋，像是裡面的水果拼盤編法，當中有從中心不斷的纏繞，編成圓形的底盤，其中利用鱗狀收編或絞編收編可使形狀單純的圓形底變成美麗出色的作品來，這些都是不同的螺旋圖，或許未來可以研究看看，或許可以發現新的螺旋性質。 | 黃彗紜 | 2021/10/7 下午 05:30:48 |
| 7 |  | 書名 自然珍藏系列—貝殼圖鑑 作者 作者：S. 彼得‧當斯 出版社 貓頭鷹出版社 簡介（摘要） 權威性的內容，清晰的照片及有系統的論述方式使本書成為包羅最齊全的新世代工具書。書中收錄500種以上、600餘幀全彩照片，作者精心安排的鑑別方法使得貝殼的辨識過程變得簡單又方便，讀者皆可藉此輕鬆蛻變成為專家。 專家執筆並加以詳細的審核，各個條目都涵蓋深入淺出的描述及附有注解的照片，突顯每個品種的特徵與鑑別重點；簡明的地圖呈現各品種的地理分布狀況。條列式套色說明欄更能瞬間加深讀者印象。 本書介紹貝殼的定義，說明貝殼分門別類的方法，並教導如何進行有系統的步驟，只要掌握重點就可以根據外形判斷貝殼的種類。書末扼要的名詞解釋更加速讀者理解專有名詞的 含義。 導讀 書中收錄全世界500多種貝殼，有些貝殼具有螺線的性質，例如：錐螺、蚯蚓錐螺、海螄螺等等。其中錐螺約有30層凸圓的螺層，從小到大依序排列，螺軸和殼口均為圓形；蚯蚓錐螺螺殼頂部呈密集盤繞，外表與錐螺很相似。我從這本書發現了許多與螺旋有關的貝殼，將來我們可以深入了解他們的數學性質。 | 王宜澄 | 2021/10/7 下午 05:21:16 |
| 6 |  | 書名 化石圖鑑：全世界500多種以上化石的彩色圖鑑最新修訂版 作者 西爾·沃克、大衛·沃德 翻譯：陳星、王原賢 出版社 貓頭鷹出版社股份有限公司 簡介（摘要） 《自然珍藏圖鑑叢書》整合全球動植物及礦物學界近年來最新的研究成果運用系統性的編輯現在賞心悅目的版面上，現在賞心悅目的版面上，是相關領域有興趣的入學者必備的基礎工具，也是有關學科的專家學者不可或缺的典藏清品。 《自然珍藏圖鑑叢書》以高解析度的現場生態攝影，配合獨創的電腦去背效果，完整呈現主題的特徵與自然神韻。金心安排的鑑別程序，輕鬆造就讀者成為專家。 導讀 這本書中有各種不同類型的化石無脊椎動物、有脊椎動物、植物等有脊椎動物中的橘石有類似等角螺旋的形狀像是未定鸚鵡螺、類空角石、連菊石等其外殼類似我們文中所討論的對應頂點軌跡。 | 沈忻穎 | 2021/10/7 下午 05:18:39 |
| 5 |  | 書名 抒心禪繞畫：104款必學圖樣+完整繪製教學 作者 佐藤心美 出版社 台灣東販 簡介（摘要） 禪繞畫是一種非常容易入門的繪畫類型，不需要特別的工具和技巧。 首先只要備好鉛筆、代針筆和紙就行了。 禪繞畫這種創作，是將圖紋加以分解，以便讓任何人都可透過反覆描繪，創造出連自己都驚訝的原創藝術。在反覆描繪的過程中，能讓自己的心靈更加平靜，並不自覺地投入在創作裡，使身心都更為專注。所以，禪繞畫不只是一種繪畫方式，還是一種藝術，也是一種平靜心靈的方式。一起拿起筆，來試試看無壓力的禪繞畫吧！ 導讀 我們從這本書裡面了解到各種纏繞畫的畫法及使用不同纏繞方法所製作出來的各式作品，其中書內有個畫法我們感覺到此螺旋有某種固定的規律，所以我們想要了解其中的數學性質。這種畫法是從三角形的角落開始往內側畫出多層三角形，不斷的往內延伸，頂點的連線有螺旋的效果在，猶如美麗的華爾滋世界，令我著迷。 | 黃慧紜 | 2021/9/27 下午 06:05:35 |
| 4 |  | 書名 這才是數學：從不知道到想知道的探索之旅 作者 作者：Paul Lockhart 譯者：畢馨云 出版社 經濟新潮社 簡介（摘要） 作者現身說法提出了他心目中的數學，應該是什麼樣子。他先談數學世界與現實世界有何不同，然後從三角形、圓、幾何、代數、三角函數、向量、到微積分，不斷地引導我們問「為什麼？」。 他和你說話，用平易近人的語氣，運用手繪的圖形，就像是自己在玩數學似的，呈現他心目中理想、有意義的數學問題，以及思考過程。他不會假裝數學很簡單，但也大方展現數學的美。在他筆下，複雜的數學概念變得符合直覺、容易掌握，數學概念不再是東一塊、西一塊，各個單元彼此可以連結，形成有意義的動人故事。他針對數學推理和古典幾何主題的討論很有意思，正呼應了他所堅信的：數學不僅是科學，也是藝術。 導讀 書中提及了「螺旋線」這個專有名詞，什麼是螺旋線呢？假想空間裡有個圓盤，水平放著，在邊緣特別標出一個點。如果我們一邊旋轉圓盤，一邊讓它垂直上升，那個特別標出的點的軌跡應該會是個完美的螺旋線。 另外，還有一些以螺旋線為中心延伸出運動軌跡的專有名詞，包括「擺線」、「內擺線」、「外擺線」以及「花輪」。擺線的概念有非常多種，包含內擺線以及外擺線。其中一個，是讓圓在另一個圓內滾動，這樣的軌跡稱為「內擺線」；當然，也可以讓圓在另一個圓的外面滾動，就成了「外擺線」。 另一個概念，是讓軌跡落在滾動原盤的內部。在內擺線的情形下，這樣會做出非常美的花輪曲線。 | 王宜澄 | 2021/9/25 下午 03:34:25 |
| 3 |  | 書名 幾何學用調查研究的方法探索 作者 本社編輯部編 出版社 九章出版社 簡介（摘要） 幾何是富有歷史且範圍廣泛的學科，可用很多種觀點來介紹。本書提供廣泛的發現式經驗而不強調演釋步驟，使讀者感到有趣又發揮其創造性。本書為學生們指引發現式的經驗，鼓勵學生利用各種器材及調查式的技巧來探討幾何觀念，適合很多不同的教學情況與方法。”調查研究(Investigation)”是以學生為中心的課程，學生可從調查研究的工作中作出積極的反應，互相分享想法與經驗。 有證據足以說明，調查研究工作對於何謂幾何可培養出一種新的態度，並且在面對數學問題的態度上也可培養出一種新的信心。本書適合閱讀對象包括中學生、師範院校學生及中學數學教師。本書很多章元整性內容提供給在職數學教師非常實用的資料庫。 導讀 這本書教導我們如何去看圖形上面的幾何數學。 我們從裡面看到他如何討論正多邊形的性質；如何利用尺規作圖畫出正多邊形，其對應頂點連線，所畫出的星狀多邊形的種類，以及利用正多邊形組成的鑲嵌圖案，讓我們了解到規律幾何圖形中的數學美感。 在書中的第五章，看到藉由動點連線在不同軌跡中的圖形變化，我們把這個點子應用在我們研究圖形問題中，並以ggb呈現動點軌跡。 | 黃慧紜 | 2021/9/25 下午 03:31:32 |
| 2 |  | 書名 數學也可以這樣學 作者 約翰．布雷克伍德( John Blackwood) 出版社 商周出版 簡介（摘要） 本書是一位任教於華德福教育體系的教師，針對七、八年級學生所發展的教程，廣獲推介引用。藉由大量圖片與作品，引導學生認識大自然、空間以及時間裡的數學。主題包括：幾何學、畢達哥拉斯及數目、柏拉圖多面體、節奏與循環。 華德福的教育方式強調學習與經驗的連結。對教師和家長而言，點燃孩子的學習熱情更勝於填鴨教學。對學生而言，概念與觀察的結合會帶來驚喜與啟蒙。數學不只是計算與公式，更是探索、興趣與應用，也是一項重要生活技能。 導讀 書中引導學生認識大自然、空間及時間裡的數學，則大自然中又藏有各式各樣的螺旋，文中不僅舉出生活裡螺旋的例子，還將繪製步驟清楚描繪在旁邊。 我在書中讀到-「阿基米德螺線」、「等角螺線」。「阿基米德螺線」(又稱為繩索螺線、拉菲草餐墊(raffia place)」這種是使用一點繩索構成的螺線，且這種螺線有個特性為，即每繞一圈，螺旋就會以相同的幅度變大一點（逐步遞增）。 至於等角螺線，我們可以運用正六邊形畫出一個簡單的「等角螺線」，則畫一系列的正六邊形，層層相套，越來越小，但按一定順序持續下去，往內會越來越小，則永遠到不了中心點，這樣的圖形中有螺旋的視覺效果。 因此我們在書中學習到各種螺旋線的圖形意義與畫法，有助於我們的研究。 | 黃慧紜 | 2021/9/24 下午 05:45:15 |
| 1 |  | 書名 跟大自然學幾何 作者 作者 : John Blackwood 譯者 : 林倉億、蘇惠玉、蘇俊鴻 出版社 商周出版 簡介（摘要） 科學是概念世界與現象世界的交織，這正是本書採取的認知模型，出發點則是幾何學。 作者約翰． 布雷克伍德曾任教於華德福教育體系，藉由細膩的觀察和巧妙的作圖，橫跨礦物界、植物界、動物界到人類世界，向讀者展示了大自然中繽紛絢爛的樣貌，探究這些多樣性是否正確反映出基本的幾何形式。 導讀 書中提及了許多關於螺旋的部分，有阿基米德螺線、等角或數對螺線等等。其中阿基米德螺線就像是一綑盤繞的繩索；等角螺線就像是髮旋、菊石化石。阿基米德螺線有一個簡單的性質 : 當以相同的角度旋轉時，半徑增加的量是一樣的；等角螺線，或稱為對數螺線， | 王宜澄 | 2021/9/24 下午 05:29:15 |
| 序號 | 截圖 | 網站簡介 | 上傳者 | 最後修改 |
|---|---|---|---|---|
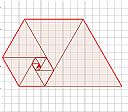
| 10 | 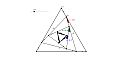 | 網站名稱 三角形固定內縮 -螺線偏移角度標示(沈忻穎) 網址 https://www.geogebra.org/classic/g6yvyyv3 網站簡介 固定長度內縮： 繪出一邊長為a的正三角形，即第一層圖形以n1表示。以點A1 沿著底邊(A1C1) 的方向平移單位向量R倍的距離，即點A2。依此類推，以同樣的規則畫出多層圖形。 固定長度內縮之螺線： 當圖形依此內縮規則向中心迭代出多層圖形後，每層圖形之頂點Ａn所連成的曲線稱為該圖形的螺線。在此行式之下，當縮放倍率R無限小時，此螺線亦會無窮地接近中心點且近似於等角螺旋，但與等比例內縮螺線的差別是固定內縮螺線的逼近速度較慢。 | 沈忻穎 | 2021/10/7 下午 02:39:43 |
| 9 | 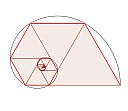 | 網站名稱 數列正三角形螺旋 網址 https://www.geogebra.org/classic/mh7auuau 網站簡介 圖形排列規則： 在起始邊長為 1 的正三角形中，以其O 點為中心，其中一邊為底邊往外畫出第二層正三角形，再接續同樣規則，畫出第三層正三角形（第一層至第三層皆為邊長為 1 的正三角形），此時第一層與第三邊長為一線段，再以此線段為底邊畫出第四層正三角形。以此類推，則這個圖形由小到大、不斷纏繞出多層正三角形，我得到了一組數列（邊長長度）為 1、1、1、2、2、3、4、5、7、9、12、16……。 | 王宜澄 | 2021/10/7 下午 01:15:09 |
| 8 | 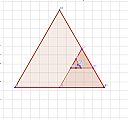 | 網站名稱 正三角形內縮螺旋-黃彗紜 網址 https://www.geogebra.org/classic/aapahcjh 網站簡介 這是我畫的正三角形內縮螺旋，如圖形中最外圍的正三角形為第一層正三角形，其頂點分別為 A1、B1、C1。 圖形排列規則： 1. 選取第一層圖形的底邊 𝐴1𝐵1 的中點（即為 A2），並以 𝐴2𝐵1 為底邊畫出第二層正三角形，此時第二層正三角形的頂點分別為 A2、B2（此時 B2 與 B1 共點）、C2。 2. 逆時針方向選取第二層圖形邊長 𝐵2𝐶2的中點（即為 B3），𝐵3𝐶2 畫出第三層正三角形。 3. 依此類推，不斷以逆時針方向，以每層正三角形邊長的一半做出下一層的正三角形。 | 黃彗紜 | 2021/10/7 下午 01:07:50 |
| 7 | 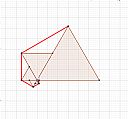 | 網站名稱 正三角形外擴螺旋-陳品妤 網址 https://www.geogebra.org/classic/vxnh4ydq 網站簡介 圖形排列規則： 1. 正三角形頂點分別為 A1、B1、C1，而點 D、E、F 分別為正三角形三邊之中點。 2. 以 A1 為中心點，P 為沿著正三角形邊長移動的動點。 3. A1 與 P 點連線，逆時針畫出第二層正三角形。 4. 接著以A1P: 𝐴1𝐵1為比值 R，在第二層正三角形對應邊的 R 倍處為 P2 點，接著以A1P2為底邊畫出 第三層正三角形，依此類推。 5. 將 B1 與所有動點（即 P、P2、P3…）連線為螺線。 | 陳品妤 | 2021/10/7 下午 01:05:32 |
| 6 |  | 網站名稱 〈黃金比例2〉：大自然的黃金比例螺線 網址 https://www.taiwannews.com.tw/ch/news/3472903?fbclid=IwAR2kwp1waokpvLmW5eS-ZrTbjOe8HhEHMY_5wAJBfnVBIfBzIdZYVM1XlTg 網站簡介 「黃金比例」一詞已經在上一篇用高跟鞋進行說明，然而這樣的黃金比例並不是人類創造的，大自然處處有匠工，有藝術之美供我們參考，存在於鸚鵡螺的「黃金比例螺線」則是人們最為熟悉的曲線。 喜歡到海邊撿貝殼的人一定看過鸚鵡螺，這顆貝殼是最能代表地球上數億年的歷史的活化石。剖開鸚鵡螺後，見圖1，美麗的螺旋曲線令人驚艷、也讓人贊嘆大自然的巧奪天工。從以下鸚鵡螺的剖面圖觀察，這條含有黃金比例的曲線，在大自然中很多地方都會出現，尤其是在貝殼、鍋牛殼等都是依據黃金比例的曲線旋轉所產的線條。 | 王宜澄 | 2021/9/28 下午 05:33:04 |
| 5 | 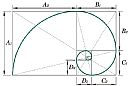 | 網站名稱 黃金螺線用希臘字母φ表示黃金比值 網址 http://www.eion.com.tw/Blogger/?Pid=1145&fbclid=IwAR0tAvvBQIv_2yDtHgAVHlt7Rc97zxGQ_IzM8QWQSsexFs93BmvPPJzKyq8 網站簡介 黃金矩形以長和寬的比為黃金分割 φ 的矩形，又稱黃金比例為數學上的比例關係。 黃金分割的比例具有藝術性、平穩與和諧的美感，使用時採取 0.618 或 1.618 計算就像圓周率在應用時取 3.14 一樣。 黃金螺線則是將黃金矩形依黃金比例的長寬比往外擴張，再將正方形頂點依序連接起來，因其螺旋狀曲線與鸚鵡螺的外殼上的螺線極為相似，此螺旋狀的曲線數學上稱為黃金螺線。 | 王宜澄 | 2021/9/28 下午 05:29:59 |
| 4 |  | 網站名稱 等角螺旋線 網址 http://www.mathland.idv.tw/ggb/ggbhtml5/logarithmic_spiral.html?fbclid=IwAR1mxCMrVIpHG51Mqeq0sn6yiNZt_BdAc9SxnHs3prYyUw4SmLsy_aTnegw 網站簡介 等角螺旋線(logarithmic spiral)是由法國數學家、哲學家 笛卡兒(René Descartes)在西元1638年發現的。瑞士數學家 雅各布·伯努利 (Jakob I. Bernoulli，1654-1705)重新研究後發現了等角螺旋線的許多特性，例如等角螺旋線擁有自我相似性，他十分驚嘆和欣賞等角螺旋線，要求將等角螺旋線的圖案雕刻在自己的墓碑上，並附上拉丁文相關語：「eadem mutata resurgo」(即使改變，依然故我)。可惜雕刻師犯錯，誤刻成阿基米德螺旋線（等速螺線）了。 | 王宜澄 | 2021/9/28 下午 05:27:14 |
| 3 |  | 網站名稱 等角螺旋線--飛鷹抓兔子的軌跡 網址 http://www.mathland.idv.tw/ggb/ggbhtml5/logarithmic_spiral1.html?fbclid=IwAR2kwp1waokpvLmW5eS-ZrTbjOe8HhEHMY_5wAJBfnVBIfBzIdZYVM1XlTg 網站簡介 飛行的老鹰緊盯定點的免子，隨視線改變，飛行方向也随之改變， 保持視線和飛行方向的夾角a°不變，則老鷹的飛行軌跡是等角螺旋線。 | 王宜澄 | 2021/9/28 下午 05:23:10 |
| 2 |  | 網站名稱 等角螺旋線--飛蛾撲火的軌跡 網址 http://www.mathland.idv.tw/ggb/ggbhtml5/logarithmic_spiral2.html?fbclid=IwAR2izHceYkNhfYV3U-AqUQBBI4u0hWblLIS-A3RyolwTBhBvWhmus59OG4Y 網站簡介 月亮距離地球遙遠，到地球的月光是平行的。 蛾在飛行時和月光線保持不變的角度，就可以直線飛行。 燭火光線是放射狀，蛾誤以為燭火光是月光，仍舊保持和燭火光線固定角度(a°)飛行，卻循等角螺旋線撲向燭火。 | 王宜澄 | 2021/9/28 下午 01:19:27 |
| 1 |  | 網站名稱 Pinterest 網址 https://in.pinterest.com/pin/601863937688099220/?fbclid=IwAR2tR9cHbgZ8wpIUN0VYrt23NX8kdDdsnpCmE5ogX7hywfEOcToulf_Sfe8 網站簡介 Pinterest，是一個網路與手機的應用程式，可以讓使用者利用其平台作為個人創意及專案工作所需的視覺探索工具，同時也有人把它視為一個圖片分享類的社群網站，用戶可以按主題分類添加和管理自己的圖片收藏，並與好友分享。其使用的網站布局為瀑布流。 我們在這個網站發現了許多外國人畫的正多邊形螺旋作品，其中網站截圖作品令我印象最深刻。它的畫法是先畫一個起始邊長為1的正三角形，接著沿著其中一邊往外畫，則這個圖形由小到大、不斷纏繞的多層正三角形，我們得到了一個數列：1、1、1、2、2、3、4、5、7、9、12、16.........，我們發現這些數列有一定的規律，目前還在了解中。 | 王宜澄 | 2021/9/27 下午 05:43:34 |
| 序號 | 書面報告 | 說明 | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 1 | | 說明 本研究探討正多邊形經不同的排列方式而作出多層不同規律排列的正多邊形後，其分割出圖形間的每層正多邊形對應頂點連接後所形成的軌跡與等角螺線之間的關聯性。 我們發現日常生活中會出現螺線，像是鸚鵡螺及蝸牛的殼切面等，想也聯想到，畫纏繞畫時利用正多邊形向內依循某種固定的規則重複且規律地畫出多層正多邊形，其圖形會產生螺旋的效果。我們想了解這些螺線中的規律性質，同時也產生一個問題：如何利用正多邊形畫出螺旋線？ 在第61 屆數學科展「同形同螺」的作品中，我們研究的螺旋規則為正n 邊形在等比例內縮與固定距離內縮的形況下，隨著內縮率越來越小，多層正多邊形頂點連線所建構出來的螺旋線會越來越接近 「等角螺線」，因此作品取名為同形同螺，即同樣的形狀下不同內縮方式卻建構出一樣的螺線。而在這次作品中，以相同正多邊形為前提下，是否可以藉由別種排列方式來找出其他形式的螺旋線？這是我們想要研究的主題，因此在名稱上加一個問號。 | 沈忻穎 | 2021/10/8 上午 11:56:11 |