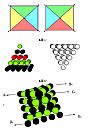
正四棱錐堆疊翻轉研究
| 專題名稱 | 正四棱錐堆疊翻轉研究 |
| 專題描述 | 本研究是個簡單有趣的小遊戲，目的是透過移動最少數量的球將正四棱錐堆疊顛倒過來。並運用國中所學到的代數，嘗試導出最簡潔的最少移動個數方程式，並推算出一般式，是本研究的亮點之處。 |
| 隊伍名稱 | 正四棱錐堆疊翻轉研究 |
| 指導老師 | 陳禹翔 呂柏辰 |
| 參賽學生 | 陳語謙 陳譔宇 |
| 延續作品 | 已上傳延續性作品說明書：20220903101957723.pdf |
| 序號 | 檔案 | 內容 | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 10 |  | 作者 陳語謙、陳譔宇、謝思宇 來源 花蓮縣第 62 屆國民中小學科學展覽會 描述 花蓮縣第 62 屆國民中小學科學展覽會研究日誌。 | 陳語謙 | 2022/9/12 下午 01:00:03 |
| 9 |  | 作者 于振華 來源 中大數學系 描述 函數，乃一種描述自變數 (independent variable) 與應變數 (dependent variable) 間的關係, 且滿足每一自變數僅對應到 (被指派到) 一個應變數的值。 | 陳譔宇 | 2022/9/11 下午 04:38:42 |
| 8 | | 作者 林宜嬪 · 張福春 來源 數學傳播 36卷4期, pp. 83-96 描述 當欲求和或乘積是屬於有理多項式的型態時, 可利用部份分式先將有理多項式分解為數個 較簡易的算式再進行對消, 可提高計算的效率, 也可避免計算上的錯誤。 而 部份分式 (partial fraction) 分解, 又稱部份分式展開, 是將有理函數分解成許多次數 較低有理函數和的形式, 來降低分子或分母多項式的次數。 分解後的分式需滿足以下條件: 1. 分式的分母需為不可約多項式 (irreducible polynomial) 或其乘冪。 2. 分式的分子多項式次數需比其分母多項式次數要低。 | 陳語謙 | 2022/9/11 下午 02:40:07 |
| 7 | | 作者 林宜嬪 · 張福春 來源 數學傳播 36卷3期, pp. 59-73 描述 :本文主要探討對消在數列的和與乘積之應用, 對消和分成四個方法: 反差分、 部份分 式、 三角函數及階乘函數進行討論。 反差分之方法又可分為下降階乘冪、 等比型及三角函數 三種型式, 其概念著重於將級數轉換為離散型之積分型式; 部份分式與三角函數主要概念著 重於對級數中的一般項進行拆解, 或藉由乘上適當的輔助量之後, 級數可以進行對消, 進而 求得解。 因階乘函數並無一般的型式, 故不作深入探討, 只提供相關例題。 對消乘積是延續對 消和的概念去探討乘積題型, 分為平方差和三角函數兩部分作介紹, 主要概念均為藉由乘上 適當的輔助量之後, 乘積可以進行對消, 進而求得解。 | 陳語謙 | 2022/9/11 下午 02:39:04 |
| 6 | | 作者 謝司宇、陳語謙、陳譔宇 來源 花蓮縣第 62 屆國民中小學科學展覽會 描述 本研究是個簡單有趣的圖形遊戲，運用硬幣排成三角形，透過移動最少數量的硬 幣，讓三角形翻轉，研究過程中透過國中所學代數，嘗試導出數學公式，並加以驗證 最少的硬幣數量是否正確以及和國小研究結果是否吻合。接著繼續研究相鄰兩層間公 差不為 1 時的情況，最後給出所有可能的情況與推導出一般式，最後繼續推廣到立體 三角錐球體堆疊的討論，算出非常簡潔的最少移動個數方程式，是本研究的亮點之 處。 | 陳語謙 | 2022/9/11 下午 02:18:02 |
| 5 | | 作者 陳語謙、沈祐睿、蔡松霖、鄭恩哲 來源 花蓮縣第 59 屆國中小科展國小組數學科第一名 描述 摘要 本研究是個簡單也有趣圖形遊戲，運用硬幣排成三角形，透過移動硬幣，讓三角形翻轉，然而移動硬幣的數量一定有最少的數量，不同層數的三角形所需要移動最少的數量也會不同，透過實際操作、記錄、推論，嘗試導出數學公式，並加以驗證最少的硬幣數量是否可正確。 壹研究動機 在一次偶然的因緣際會下，我們被老師問到了一個數學題目，用硬幣排出三角形，並嘗試移動硬幣，看如何以最少的數量，讓三角形翻轉，一開始滿簡單，等硬幣數量開始增加，三角形也越來越多層之後，就感覺有些挑戰，嘗試解了幾題後，就想要多了解這個遊戲，並希望可以繼續解開有關這個題目的所有問題，找出解題的方法，因此我們找老師來研究翻轉金字塔，我們研究這個是想要（一）了解與尋找翻轉金字塔遊戲的規律（二）嘗試破解遊戲的方式（三）運用所學過的四則運算，嘗試找出相對應的數學公式，計算出移動最少硬幣的個數，所以如果我們要完成這些目標，就要試著把數學公式導出來，才能解決。 | 陳語謙 | 2022/9/11 下午 02:17:21 |
| 4 | | 作者 蘇俊鴻 來源 科學發展 2011年3月，459期｜ 描述 路米司（Elisha Scott Loomis, 1852-1940）所著的《畢氏定理》 一書，收集了370個有關畢氏定理的各式證法。會有這麼多的證明， 是因為在中世紀時，大學畢業生必須能找到一種新的證法才能得到 學位。 | 陳語謙 | 2022/9/11 下午 02:12:39 |
| 3 | | 作者 宋蕙君、 陳柏揚、謝明君 來源 中華民國第四十八屆中小學科學展覽會 作品說明書 描述 (一)直角三角形中以直角邊為邊長的兩個正方形面積之和等於以斜邊為邊長之正方形的面 積。 (二)直角三角形斜邊長度的平方等於兩個直角邊的長度平方和。 (三)一般而言，西方國家都用「畢達哥拉斯定理」(Pythagorean Theorem)此名稱。在我國， 有時簡稱其為「畢氏定理」，有時亦用「商高定理」、「勾股定理」或「勾股弦定理」 等名稱，在中國古代，此定理便已被發現，遠較畢氏為早。 | 陳語謙 | 2022/9/11 下午 02:12:05 |
| 2 | | 作者 陳冠宏 來源 信望愛文教基金會 描述 本作品主要是在介紹柯西不等式。 | 陳語謙 | 2022/9/11 下午 02:11:47 |
| 1 | | 作者 陳學儀 來源 台北市立第一女子高級中學 描述 因為直角三角形有畢氏數和畢氏數製造機 (m2 − n2, 2mn, m2 + n2), 我們猜想其他的三角 形是否也有這些特殊的關係, 所以決定從夾角 120 度的整數邊三角形著手, 希望能找出類 似畢氏數製造機, 或是其整數邊長解的規律, 並從一組整數解推出其他組解. | 陳語謙 | 2022/9/11 下午 02:09:49 |
| 序號 | 封面照 | 內容說明 | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 10 |  | 類別 相簿集 名稱 研究日誌 說明 我們在做科展時的研究日誌。 | 陳語謙 | 2022/9/22 下午 04:26:24 |
| 9 |  | 類別 相簿集 名稱 撰寫本文 說明 向評審展現我們的想法 | 陳譔宇 | 2022/9/21 下午 04:48:08 |
| 8 |  | 類別 相簿集 名稱 正四棱錐的翻轉定義 說明 正四棱錐的翻轉定義 | 陳語謙 | 2022/9/20 下午 04:50:40 |
| 7 |  | 類別 相簿集 名稱 線上討論 說明 因為今年疫情無法到學校討論，所以我們變成以線上Google Meet的方式來討論，我們在這個周末，發現保留顆數都是以3層的模式出現，並找出了最多的不移動顆數的公式。 | 陳語謙 | 2022/9/17 下午 05:59:28 |
| 6 |  | 類別 相簿集 名稱 gsp正四棱錐 說明 我們運用2D繪圖軟體來繪製不同層數的正四棱錐，以來觀察其中的規律。 | 陳譔宇 | 2022/9/15 下午 04:36:13 |
| 5 |  | 類別 相簿集 名稱 鐵珠正四錐棱模型 說明 在這次的科展老師幫我們買來鋼珠和一種長條的磁鐵，讓我們能夠更容易的去找出公式，且這個模型可以拆掉、重組，所以比保麗龍球好用。 | 陳語謙 | 2022/9/14 下午 04:41:11 |
| 4 |  | 類別 相簿集 名稱 保麗龍球三角錐模型 說明 在我們比科展的時候，我們利用保麗龍球來當作我們三角錐的模型，藉此可以更方便找出公式，並完成研究。 | 陳語謙 | 2022/9/14 下午 04:29:31 |
| 3 |  | 類別 相簿集 名稱 製作Sketchup圖檔 說明 利用了3D的繪圖軟體-sketchup來幫助我們進行計算正四棱錐。 | 陳語謙 | 2022/9/13 下午 04:36:15 |
| 2 |  | 類別 相簿集 名稱 討論 說明 討論 | 陳語謙 | 2022/9/8 下午 04:56:16 |
| 1 |  | 類別 相簿集 名稱 找資料 說明 找資料 | 陳語謙 | 2022/9/8 下午 04:55:57 |
| 序號 | 內容 | 上傳者 | 最後修改 |
|---|---|---|---|
| 10 | 作者 陳語謙 標題 製作書面報告(9/20) 內容 看著「相關連結」、「檔案庫」、「藏書閣」……的左邊，全部從紅色變成綠色的，讓我非常開心，經過了這麼久的研究，我們終於只要製作書面報告。有了前兩次的經驗，感覺這一次做本文比之前更容易啊 ! | 陳語謙 | 2022/9/20 下午 08:08:03 |
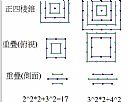
| 9 | 作者 陳譔宇 標題 應證想法(9/20) 內容 我們在觀察的時候，發現層層互換的方式有很多種，但是我們觀察了4到8層的圖形後，發現最底層和倒數第3層互換，保留的顆數會最多。這一點和科展時研究的不一樣，因為科展時互換，每個層數都不一樣，但是正四棱椎都是同一層。真的是太神奇了。 | 陳譔宇 | 2022/9/20 下午 04:44:08 |
| 8 | 作者 陳譔宇 標題 推導公式(9/18) 內容 在這一個禮拜，老師要我們和科展一樣利用相同的方式，使用另一個繪圖軟體-gsp，只不過是2D的。讓我們更容易地去推導公式。之後我們觀察了4~8層的正四棱錐後，發現不移動顆數都是由3層的形式出現，所以我們很快的推導出了可以算出不移動顆數的公式。 | 陳譔宇 | 2022/9/18 上午 10:22:23 |
| 7 | 作者 陳語謙 標題 製作實體模型 內容 在我們比科展的時候，我們利用保麗龍球來當作我們三角錐的模型，藉此可以更方便找出公式，並完成研究。在這次的科展老師幫我們買來鋼珠和一種長條的磁鐵，讓我們能夠更方便的去找出公式，且這個模型可以拆掉、重組，所以比保麗龍球好用。 | 陳語謙 | 2022/9/14 下午 04:47:01 |
| 6 | 作者 陳語謙 標題 製作圖檔(9/13) 內容 為了更方便的推算出正四棱錐的公式，我們嘗試用3D的繪圖軟體-sketchup來畫出我們的正四棱錐。我們試著透過把同一個立體圖形複製後和原本的圖形重疊，發現讓它們中間的部分重疊的移動顆數是最少的。 | 陳語謙 | 2022/9/13 下午 01:04:17 |
| 5 | 作者 陳譔宇 標題 撰寫本文(9/13) 內容 現在只剩下本文還沒有亮綠燈了！所以接下來就是要打本文了，希望我們可以把公式推導出來，完成本文的部分。 | 陳譔宇 | 2022/9/13 下午 01:04:07 |
| 4 | 作者 陳譔宇 標題 完成藏書閣(9/12) 內容 我們終於把藏書閣放滿書了，其間困難重重，因為在網路上查都查不太到跟相關我們主題的書，就算有查到也是教科書或參考書，還有英文的原文書。 | 陳譔宇 | 2022/9/12 下午 10:09:47 |
| 3 | 作者 陳語謙 標題 完成檔案庫、相關連結(9/12) 內容 今天我們把檔案庫、相關連結都變成綠燈了，到這個月底前(9/30)，我們要把本文打完。希望我們能做完，下禮拜就要開始做本文了! | 陳語謙 | 2022/9/12 下午 01:11:33 |
| 2 | 作者 陳譔宇 標題 9/8文獻探討 內容 首先我們先在網路上找尋跟我們題目有相關的文獻，但是我們遇到了一個挫折，就是這一類型的文獻真的是少之又少。但是我們也有從中找到一些和函數有關的相關資料，希望可以對我們的研究有所幫助。 | 陳譔宇 | 2022/9/8 下午 01:08:34 |
| 1 | 作者 陳語謙 標題 9/8決定內容 內容 這次的主題我們是延續上一次科展的題目，上一次的科展我們研究相鄰兩層間公差不為 1 時的情況，最後給出所有可能的情況與推導出一般式，最後繼續推廣到立體三角錐球體堆疊的討論。在這一次的小論文，我們想讓研究變更完整，所以我們接著準備開始做不同錐體的翻轉研究。 | 陳語謙 | 2022/9/8 下午 01:00:23 |
| 序號 | 封面 | 簡介（摘要） | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 10 |  | 書名 Essays on SIGMA: Simulation and Implementation of General Mathematical Activity 1st Edition 作者 約翰·S·N·埃爾維 出版社 CreateSpace Independent Publishing Platform 簡介（摘要） These Essays embody a comprehensive scheme for the development of a database for research in all areas of Mathematics. The underlying mathematical computer processor proposed, called SIGMA, is seen as providing an interactive research environment. The application of arbitrary theorems to well-formed expressions constitutes the basic activity within this environment and the goal is to produce theorems which are formulated in maximally operational and constructive modes. This presents a huge challenge to mathematical ingenuity and technique and it is proposed that it is pursued internationally through a dedicated Institute. 導讀 The Essays on SIGMA furnish a substantial foundation for this crucially important enterprise. | 陳譔宇 | 2022/9/12 下午 01:07:39 |
| 9 |  | 書名 少年Galileo觀念數學套書1：對數／三角函數／虛數／微分與積分（共4冊） 作者 日本Newton Press 出版社 人人出版 簡介（摘要） 碰到棘手的數學難題，若不能先把答案解出來，就無法挑戰更進階的題目，在學習上更是如此。「少年伽利略」就是用一貫的精美圖解，以淺顯概念摘要出重點，不論是複習或預習，都適合國高中生建立清晰的觀念，等基礎打好了，就能繼續往下一步前進，再加上輕薄的內容，讓學習減少負擔。 導讀 數學的發展，都是因應實際需求的結果，指數與對數也不例外。在航海、商業、天文等計算，往往涉及龐大的數字，如果像440000000000000000000000000這樣的數字，光是用看的就已經眼花撩亂，更別說要計算了。但若運用指數的概念，寫成 4.4×10^26就方便多了。而我們生活周遭熟悉的分貝和酸鹼值，其實也運用了對數的概念。 指數與對數的應用十分廣泛，但是概念本身有些抽象難懂的地方，只要多以實際例子輔佐學習，就能釐清概念，更容易吸收。 | 陳譔宇 | 2022/9/12 下午 12:55:39 |
| 8 |  | 書名 數學奧林匹克小叢書.高中卷.平均值不等式與柯西不等式 作者 李勝宏 出版社 華東師範大學出版社 簡介（摘要） 本書主要介紹平均值不等式和阿西不等式。用不同的方法證明了這兩個基本的不等式，並涉及證明一般不等式問題的常用方法和技巧。同時介紹了幾個常見的著名不等式，如排序不等式、赫爾德不等式、契比雪夫不等式和閔可夫斯基不等式，內容豐富、全面。 導讀 重點介紹了平均值不等式與柯西不等式在證明不等式和求最值等問題中的應用。本書所討論的題目，大多是國內外數學競賽試題，具有一定的代表性，其證明有一定的技巧。 | 陳譔宇 | 2022/9/12 下午 12:52:25 |
| 7 |  | 書名 三角函數：sin、cos、tan 人人伽利略19 作者 日本Newton Press 出版社 人人出版 簡介（摘要） 三角函數的基礎是正弦sin、餘弦cos、正切tan，雖然令許多學生頭痛不已，卻是相當基礎且重要的數學定理，其用處無遠弗屆。 從古代天文學的三角測量開始，到如今網路影片、地震速報，三角函數的應用早已涵蓋工程學、航海學、測繪學、音樂、物理、天文、地震分析，甚至是目前的網路影像與聲音壓縮、合成等等，堪稱是現代生活中各種技術的必備基礎。具備良好的數學運算能力，也有助於整合觀念，培養邏輯清晰的推理能力。 導讀 有鑑於此，本書以「三角函數」為主題，運用大量精彩圖片，有系統且循序漸進的方式，從三角形的性質開始談起，逐步解說三角函數的起源、基礎、公式、用途，並擴及廣泛應用於各領域的代表性工具「傅立葉分析」、「量子力學」、相關的數學公式等。其中還特別附上三角函數的練習題，供讀者自我測驗，是內容相當豐富且全面性的三角函數專書，不但可幫助學生打穩基礎，對想進一步學習的讀者或老師，想必也能有所裨益。尤其本書中所列出各步驟的計算過程和解說，最有助於解開艱澀難懂之處，是市面上難得一見的數學讀本。 | 陳譔宇 | 2022/9/12 下午 12:48:23 |
| 6 |  | 書名 微分與積分：讀過就能輕鬆上手！ 少年伽利略6 作者 日本Newton Press 出版社 人人出版 簡介（摘要） 微積分是許多理工、商學院學生都要修讀的基礎課程。而且，微積分的應用非常廣泛，從土地面積到哈雷彗星軌道的預測、拋物線的計算，都要用到微積分。微積分學得好，整個學習的歷程會更順利、更愉快。這也是《微分與積分：讀過就能輕鬆上手！》出版的用意 導讀 從微積分的誕生開始，探求23歲的牛頓構想微積分的思考脈絡，從微分跟積分的角度講解重要公式，循序漸進，加上大量精美的圖解，最後再整理重要公式，讓讀者更容易掌握微積分的概念。 | 陳譔宇 | 2022/9/12 下午 12:46:13 |
| 5 |  | 書名 【新裝版】3小時讀通幾何 作者 岡部恒治, 本丸諒 出版社 世茂 簡介（摘要） 尼羅河的氾濫，會讓此前的土地規劃一下子就泡湯，使人們必須重新測量土地。 「土地測量」在古希臘語（土地γη、測量μεϰρεω）中叫做geo（土地）metry（測量），一般是認為，geo的發音被轉變為漢語後，就被稱做「幾何」。 源於土地測量的幾何學是在求取三角形、四邊形、圓或四角錐（金字塔）等圖形之面積或體積的過程中，慢慢連串起來的學問。 幾何的進一步應用，則從橡膠幾何（拓撲學）、以蕨類植物的葉脈或河川的分布為對象的碎形幾何學、一直到可以聯繫到宇宙形狀的龐加萊猜想等，不愧是「最先端的數學」。 讓我們配合易懂的插圖，敲開幾何世界的大門吧。 導讀 「只要會畫圖，就會幾何！」 「證明題不再是難題！」 「體驗幾何解題樂趣！」 透過「用畫圖來表示」的方式，將複雜的內容具體化，學會看穿「問題本質」的能力。 從理論到實際應用，甚至艱深的「三角函數」與「微積分」也變得有趣了！ | 陳譔宇 | 2022/9/6 下午 04:51:08 |
| 4 |  | 書名 數學特訓營：7天搞定高中數列與不等式 作者 莊肅欽 出版社 浙江大學出版社 簡介（摘要） 本書我們以數學思想方法為主線展開，兼顧基本知識結構，重點向同學們介紹解決有關數列與不等式問題的基本策略與方法，並在各標題的擬定時，就力圖開宗明義的點明每天及各課時的學習主題與重點，採用 「定點清除」，以數學特訓營的形式，通過7天，18堂課幫助大家搞定高中數列與不等式！ 導讀 學習數學的目的是什麼？ 或許有些同學還沒有深入思考過這個問題，有些同學會說，是為了學習一些數學知識，有些同學的目的會更加直接，就是為了考上一所好大學。 當然，這些想法都無可厚非而且也是必須的，問題是，我們學習數學的目標卻不僅僅就是這些，我們既要學習一些必要的數學基礎知識，又要掌握一些解決問題的策略與方法，更重要的是，在學習數學的過程中培養自己良好的學習習慣和科學的思維方法，養成規范、嚴謹、准確、科學、條理、理性等良好的個性品質。 這會對你一生的學習、工作和生活產生巨大的影響。基於這樣的目標，本書我們以數學思想方法為主線展開，兼顧基本知識結構，重點向同學們介紹解決有關數列與不等式問題的基本策略與方法，並在各標題的擬定時，就力圖開宗明義的點明每天及各課時的學習主題與重點，務請同學們仔細揣摩和玩味。 期待同學們在完成對本書的研究后能有這樣的感受：數學就是生活，解決數學問題與解決現實生活問題一樣有着相同的思維方法，總是遵循這樣幾個基本原則:復雜問題簡單化，陌生問題熟悉化，抽象問題直觀化。 因為，在這些朴素的道理中蘊含着重要的數學思想方法，如轉化與化歸思想、數形結合思想等。 在學習數學的過程中，你不可能做遍所有的數學題，要提高學習效率，輕松學好數學，就需要總結和把握問題的基本特征和思維規律，實現舉一反三的學習，這正是本書所努力闡述的思想。 | 陳譔宇 | 2022/9/6 下午 04:46:35 |
| 3 |  | 書名 畢氏定理四千年 作者 Eli Maor 出版社 三民 簡介（摘要） 畢氏定理是所有（無論理論還是應用）科學的基石。毛爾重現畢氏定理在數學史上的關鍵要角，為這流傳許久的數學遺產增添許多繽紛色彩。 導讀 作者毛爾 (Eli Maor) 在此書中重述畢氏定理故事的許多面向，書寫紮實，極富洞察力。他指出畢達哥拉斯證得畢氏定理的千餘年前，巴比倫人就已經發現勾股間巧妙的數學關係。畢達哥拉斯也許是證明畢氏定理的第一人。 | 陳譔宇 | 2022/9/6 下午 04:42:46 |
| 2 |  | 書名 翻轉微積分的28堂課：從瞬間到永恆，探索極限、縱橫運算、破解定理，圖解思考萬物變化的數學語言 作者 畢馨云 出版社 臉譜 簡介（摘要） 本書前半部談的是「瞬間」，探討導數的故事。我們會思索一毫米的月球軌道、一小口的奶油吐司、一粒粉塵的不規則跳躍，以及一隻狗剎那間的決定。 本書後半部談的是「永恆」，運用積分匯聚成流的力量。我們會遇到一個由微小薄片構成的圓、一支由無數士兵組成的軍隊、一條由千篇一律的樓房形成的天際線，以及一個布滿十億兆顆星星的宇宙。 導讀 最棒的數學模型可以幫我們打造即將問世的暢銷書嗎？包括這一本！ 要探究歷史的法則必須討論積分？要解答最佳化問題得用迴紋針？ 理查・費曼是怎麼在充滿惡作劇魔法的數學遊樂場裡學微積分？ 經濟學家嘗試發展幸福計算法，微積分可以解釋我們的快樂與痛苦嗎？ 數學家為什麼同情球形，而不是三角形、長方形？ 福爾摩斯式推論其實是高等數學，解開謎題的瞬間微積分就勝利了？！ | 陳譔宇 | 2022/9/6 下午 04:38:30 |
| 1 |  | 書名 Excel 公式+函數職場專用超級辭典【暢銷第二版】：新人、老鳥到大師級都需要的速查指引 作者 王國勝 出版社 PCuSER電腦人文化 簡介（摘要） 【11大類函數全面收錄】 三角函數、日期與時間函數、資料庫函數、財務函數、統計函數、文字函數……等 【函數一堆不知道怎麼用？】 分門別類用途更清晰，公式範例教你如何舉一反三 【職場高手必學超級函數】 財務、人資、業務、學校必學各項函數，讓工作輕鬆完成 【一書在手速查函數功能】 函數太多記不住？本書收錄大量函數與簡潔教學，不花心力輕鬆查看 導讀 本書精選11大類，360個常用函數，幾乎在各行各業會用到的函數都有收錄！ 每個函數與公式底下皆有範例教你怎麼使用，簡單易懂讓你不需要花太大心力即可理解，跟著做馬上學會如何用！ 書中收錄的函數都是小編實測在台灣版Excel中有實際包含的函數，每個都在各行各業中被頻繁使用，還可以互相搭配讓函數功能更強大！ | 陳語謙 | 2022/9/6 下午 04:24:58 |
| 序號 | 截圖 | 網站簡介 | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 10 |  | 網站名稱 四面體 網址 https://zh.wikipedia.org/zh-tw/%E5%9B%9B%E9%9D%A2%E9%AB%94?fbclid=IwAR0jeNJRmX76EYoAtZ2kQ7zWOswWQpMKiCOQwSaHE9jKiX0JL2FNhU_CtTQ 網站簡介 四面體是由四個三角形面組成的多面體，每兩個三角形都有一個共同的邊，每三個三角形都有一個共同的頂點。四面體有四個頂點，六條棱，四個面，是所有凸多面體中最簡單的。四面體包括正四面體、鍥形體等種類，由四個全等的正三角形組成的四面體稱為正四面體。四面體也可以依角的類型分為銳角四面體、鈍角四面體、和直角四面體。 | 陳譔宇 | 2022/9/21 下午 04:45:35 |
| 9 | 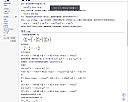 | 網站名稱 Σ 網址 https://zh.m.wikipedia.org/zh-tw/%CE%A3 網站簡介 Sigma（大寫Σ，小寫σ，中文音譯：希格瑪），是第十八個希臘字母。在現代的希臘數字代表200。 大寫Σ可以表示： 數學上的求和符號（又稱和式號）。 粒子物理學中的一類重子（Σ重子）。 小寫σ可以表示： σ鍵，化學上一類原子軌道「頭碰頭」形成的化學鍵。 統計學上的標準差。 除數函數。 σ-代數。 RNA聚合酶的σ因子。 恆星光度的 斯特藩-玻爾茲曼常數。 應力。 西里爾字母的С及拉丁字母的S都源於Sigma，而西里爾字母С的直接起源是Sigma的一個彎月形變體Ϲ。 | 陳譔宇 | 2022/9/8 下午 12:39:17 |
| 8 |  | 網站名稱 翻轉金字塔 網址 https://contest.hlc.edu.tw/science/publish/upload/108-A101.pdf 網站簡介 本研究是個簡單也有趣的圖形遊戲，運用硬幣排成三角形，透過移動硬幣，讓三角形翻 轉，然而移動硬幣時一定會有最少的數量，不同層數的三角形所需要移動的最少數量也會不 同，透過實際操作、記錄、推論，嘗試導出數學公式，並加以驗證最少的硬幣數量是否正 確。 | 陳譔宇 | 2022/9/8 下午 12:37:51 |
| 7 |  | 網站名稱 GSP融入數學幾何學習(GSP入門教學) 網址 https://www.youtube.com/watch?v=i3O-NlBezGQ 網站簡介 國二、三學生 先備知識：知道常見幾何圖形的定義，瞭解平行、中垂線定義。 | 陳譔宇 | 2022/9/7 下午 01:11:58 |
| 6 |  | 網站名稱 柯西-施瓦茨不等式 網址 https://zh.wikipedia.org/zh-tw/%E6%9F%AF%E8%A5%BF-%E6%96%BD%E7%93%A6%E8%8C%A8%E4%B8%8D%E7%AD%89%E5%BC%8F 網站簡介 數學上，柯西-施瓦茨不等式，又稱施瓦茨不等式或柯西-布尼亞科夫斯基-施瓦茨不等式，是一條很多場合都用得上的不等式；例如線性代數的矢量，數學分析的無窮級數和乘積的積分，和機率論的變異數和共變異數。它被認為是最重要的數學不等式之一。它有一些推廣，如赫爾德不等式。 不等式以奧古斯丁·路易·柯西（Augustin Louis Cauchy），赫爾曼·阿曼杜斯·施瓦茨（Hermann Amandus Schwarz），和維克托·雅科夫列維奇·布尼亞科夫斯基（Виктор Яковлевич Буняковский）命名。 | 陳譔宇 | 2022/9/7 下午 01:01:03 |
| 5 |  | 網站名稱 函數 網址 https://zh.wikipedia.org/zh-tw/%E5%87%BD%E6%95%B0 網站簡介 若{\displaystyle x}x是實數，以有序對 {\displaystyle (x,\,x^{2})}{\displaystyle (x,\,x^{2})} 為元素所構成的集合就是一個函數。直觀上代表＂輸入＂ {\displaystyle x}x 就可以得到唯一值 {\displaystyle x^{2}}x^{2} 的對應關係。 一般會以英文字母 {\displaystyle f,\,g,\,h}{\displaystyle f,\,g,\,h} 表示函數，並把 {\displaystyle x}x 依據函數 {\displaystyle f}f 的對應規則所得到的值寫作{\displaystyle f(x)}f(x) ，並讀作"f of x"。函數的概念不限於數之間的對應關係，例定義函數 {\displaystyle \operatorname {Capital} }{\displaystyle \operatorname {Capital} } 為世界上所有國家跟它現在的首都的對應關係，那輸入英國就會輸出唯一值倫敦：{\displaystyle \operatorname {Capital} (\mathrm {U.K.} )=\mathrm {London} }{\displaystyle \operatorname {Capital} (\mathrm {U.K.} )=\mathrm {London} }。 直觀上的"多變數函數"其實也可以概括到一般函數的定義裡。例如算式 {\displaystyle x\times y}{\displaystyle x\times y} 有兩個實數參數 {\displaystyle x}x 和 {\displaystyle y}y。可以將這兩個參數看作一個實數有序對 {\displaystyle (x,y)}(x,y) ，然後定義一個以 {\displaystyle ((x,\,y),\,x\times y)}{\displaystyle ((x,\,y),\,x\times y)} 為元素所構成的函數 {\displaystyle f}f ，然後把 {\displaystyle f[(x,\,y)]=x\times y}{\displaystyle f[(x,\,y)]=x\times y} 簡記成符合直觀的 {\displaystyle f(x,\,y)=x\times y}{\displaystyle f(x,\,y)=x\times y} 。 數學中，對應、映射、轉換通常都是函數的別稱，但也可能有別的意思，如在拓撲學的映射有時代表的是連續函數。 在類型論的λ演算中，"對應關係"可以是作為一個原始概念(也就是無定義名詞)，而不像上述的定義把函數視為集合的衍伸物。 | 陳譔宇 | 2022/9/7 下午 12:59:30 |
| 4 |  | 網站名稱 一些球堆成三角形.第一个是一个球,摆成了球形,第二个是用3个圆堆起来的三角形,第三个是用6个圆堆起来的三角形,第4个是9个圆堆起来的三角形……你知道第5堆有多少个小球吗?第8堆呢? 網址 http://5lishi.com/huaxue/2019-09-18/97059.html 網站簡介 一些球堆成三角形.第一个是一个球,摆成了球形,第二个是用3个圆堆起来的三角形,第三个是用6个圆堆起来的三角形,第4个是9个圆堆起来的三角形……你知道第5堆有多少个小球吗?第8堆呢? | 陳譔宇 | 2022/9/7 下午 12:52:38 |
| 3 |  | 網站名稱 微積分誕生的前奏，超級絕妙的中國古代堆垛術 網址 https://kknews.cc/zh-tw/history/2y8gkmz.html 網站簡介 沈括是我國宋朝著名科學家，宋代制酒業很發達，為了存儲方便，酒缸是要一層一層堆起來的，形成了堆垛，怎樣用簡便的方法算出堆垛中酒缸的總數，古代稱之為堆垛術．沈括用了近十年的時間寫了著名的《夢溪筆談》，隙積術和會圓術是沈括在數學領域的兩大重要研究成果，隙積術是用來計算諸如累棋、層壇、積罌（堆砌的酒罈子）一類堆垛物體的體積公式，其中包含了高階等差級數的計算公式；會圓術是計算圓弧的弦、矢（弧的高）與孤長間數量關係的數學公式。 原文網址：https://kknews.cc/history/2y8gkmz.html | 陳譔宇 | 2022/9/7 下午 12:50:51 |
| 2 |  | 網站名稱 AutoCAD 3D繪圖(19)__堆疊圓珠組 網址 https://liuyunantw.pixnet.net/blog/post/461018798-autocad-3d%E7%B9%AA%E5%9C%96(19)__%E5%A0%86%E7%96%8A%E5%9C%93%E7%8F%A0%E7%B5%84?fbclid=IwAR1M7Jk8bg_DlptR-SBcDBAxZtBKvv25O5Ss0WRe1HYWzx6ciyPEicihybM 網站簡介 在AutoCAD中要畫3D組立圖有對齊指令可以用，可以很快對齊放置3D物件。遇到真正3D圓球時對齊指令無用武之地，在R14版之前3D圓球連可以對齊用的參考點都沒有，R14版之後能提供對齊參考的點只有球心 圓球堆疊的問題在許多3D繪圖軟體幾乎都是難題，因為能用的參考點都是只有球心。同樣的問題我在畫Solid Edge時就遇過，用的解決方法和AutoCAD畫法相同，都是另外畫出輔助對齊用的草圖來處理 | 陳譔宇 | 2022/9/7 下午 12:40:55 |
| 1 |  | 網站名稱 筆試題的思考：移動最少硬幣讓金字塔上下倒過來 網址 https://kknews.cc/zh-tw/education/4mmpjnv.html 網站簡介 用硬幣擺成金字塔，要移動儘可能少的硬幣讓金字塔上下倒過來，對於 4 層金字塔只要移動圖中 3 個藍色的硬幣即可。最後一層左右兩側各移動 m 個硬幣後，最後一層還剩餘 n-2*m 個硬幣，需要從上面依次往下移動 n-2*m 個硬幣、n-2*m-1 個硬幣、……（遞減直到最終為 1 個硬幣） 按照上面的方法同樣可以分析出 6 層金字塔最少需要移動多少個硬幣，此處不再詳述，大家可以自己分析一下，下面直接給出各個方案移動硬幣數分別為15， 8， 7， 12（移動 12 個硬幣是最後一層左右兩側各移動 3個硬幣的情況）。 通過分析我們可以得出 6 層金字塔最少需要移動 7 個硬幣。但我們總不能一直這樣分析吧！對於層數少的可以自己分析，層數太多例如 100 層怎麼辦？而且一開始我也說了這是有通解的。這個時候很自然的就可以想到靠機器來幫我們做苦力。 | 陳語謙 | 2022/9/3 下午 12:32:33 |
| 序號 | 書面報告 | 說明 | 上傳者 | 最後修改 |
|---|---|---|---|---|
| 1 | | 說明 本研究是個簡單有趣的小遊戲，目的是透過移動最少數量的球將正四棱錐堆疊顛倒過來。並運用國中所學到的代數，嘗試導出最簡潔的最少移動個數方程式，並推算出一般式，是本研究的亮點之處。 | 陳語謙 | 2022/9/29 下午 04:45:12 |