藏在方格裡的智慧：魔術方陣的歷史與規則

專題名稱藏在方格裡的智慧：魔術方陣的歷史與規則

專題描述在日常生活中，我們對數學特別有興趣。偶然間，我們看到金庸小說射鵰英雄傳\上有一個很特別的數學題目「九宮之義，法以靈龜，二四為肩，六八為足，左三右七，戴九履一，五居中央」，於是我們去查了這個數學題的原理，發現是數學上的魔方陣。我們覺得很神奇，魔術方陣是一種古老且神奇的數字排列的遊戲，而它最大的特色就在於每一行、每一列與對更深入的了解魔方陣。 透過這次小論文，我們想從數學的角度研究不同的魔方陣和它們基本原理，且了解它的歷史與應用。
　　魔方陣是古人發明的一種九宮格數字遊戲，而它最大的特色就在於每一角線上的數字總和都相等，而它雖然看似簡單，但其中卻隱藏著深奧的數學規律。觸動我們想行、每一列與對角線上的數字總和都相等，而它雖然看似簡單，但其中卻隱藏著深奧的數學規律。而早在四百多年前，中國的「洛書」中就出現了九宮格魔術方陣，也在金庸小說中也有提到，因此我們對此產生好奇，並想深入探討，所以我們在這次的小論文中會了解不同的魔術方陣種類、規則、歷史背景以及生活應用。

隊伍名稱數陣天啟

指導老師林瑋儒　

參賽學生趙向　王顗嫣　張羽涵　劉宥陞

序號檔案內容上傳者最後修改
4作者 林克瀛
來源 清華大學物理系
描述 研究動機：
從小我就喜歡各種數學遊戲，像是魔方陣和棋盤題目，而「騎士巡邏」這個經典問題更讓我著迷。這次想把兩個古老的數學遊戲結合起來，看看能不能在有趣的挑戰中找到新的數學規律，讓枯燥的計算變得更有趣。
研究目的：
這個研究的目的是想設計出一種特別的棋盤排列，讓它同時符合魔方陣的規則（每行每列和對角線數字和都相等），又能安排一條騎士巡邏路徑走遍所有格子。希望藉此找出兩種經典數學問題的連結，感受數學結構的美感。
研究方法：
我先畫出棋盤並安排魔方陣的數字，接著用圖論和路徑設計的想法，試著規劃一條騎士能走遍所有格子的完整路徑。過程中不只靠嘗試，也用數學推理和對稱分析來檢查排列是否可行，減少隨機亂試的時間。
討論：
結果發現，騎士巡邏和魔方陣的結合並不容易，但當找到符合條件的排列時，能看到棋盤裡隱藏的數學對稱和巧妙設計，讓人對數學結構的美有更深的體會。這個過程不僅增添數學樂趣，也讓我學到更多用邏輯推理解決問題的方法。
劉宥陞2025/8/31 下午 09:04:42
3作者 黃欣怡、徐麗萍
來源 中華民國第 52 屆中小學科學展覽會
描述 （一）研究動機
自從進入國中後，學校推行閱讀運動，而是平時大量使用電腦的作者慢慢的開始閱讀書中的文字，而一次偶然的機會，作者在圖書館中看到了金庸小說的射鵰英雄傳，閱讀過後發現書中有一個很有趣的數學遊戲，作者在好奇心的驅使下，詢問老師過後對魔方陣也有了初步的了解，最後在老師的邀請下決定參加了科展比賽。
（二）研究目的
主要在瞭解魔方正的種類，並找出魔方正的解法，最後探討三階的魔方陣。
（三）研究方法
查詢資料了解魔方陣的歷史，並利用斜角注記法找出魔方陣的解法，最後，透過實際測驗來更進一步的了解三階的魔方陣。
（四）研究結果
綜合上面的方法，中心為59的3階質數魔方陣定和為最小（ 如圖十三所示 ）。魔方陣的填製方法並唯 一 ，雖然以上所研究的方法，可以幫助我們解出魔方陣，但是不同的方法，亦可找到不同的解答，這 次數學科展，在群策群力下，我們找到了解答，不過，還沒有辦法像先前探討的魔方陣解法一樣，能夠 有一套快速的記憶公式，讓我們能很快找到答案。		張羽涵2025/8/26 下午 08:25:05
2作者 林志杰
來源 臺灣博碩士論文知識加值系統
描述 一個泛魔方陣是指在一個表格中填入從1到n平方的連續整數,使每行、每列和所有對角線上的數字總和都相同的表格。		趙向2025/8/25 下午 11:18:09
1作者 高婕瑄 許舒涵
來源 中華民國第四十七屆中小學科學展覽會
描述 (一)研究動機
高一老師給了「論保其壽的渾圓圖」此份報告，裡面從渾圓圖的淵源開，在文末附了各式的渾圓圖，有別於我們一般常見的正方形方陣，於是我們不禁開始思考，若將魔方陣由正方形改為三角形或是其他形狀，是否都會有解？並且會有著正方形方陣所不具有的性質？研究魔方陣的變形，並期望變形後的魔方陣可以運用在更多不同的領域。
(二)研究目的
探討另類魔方陣的解，試著找出能任意填出解的方法，從 n 階推至(n+1)階，並推廣至平
面 m 邊形及立體。
(三)研究方法
利用試誤法後觀察規律，並融入所學加以驗證。
(四)討論
我們一開始的遊戲限制是為了簡化解的情形，以便於討論，但就我們的填法而言，主要核心概念是利用順逆時針及連續數字的特性進行求解，因此一開始遊戲沒有做那樣的假設依然有解。而根據我們的填法，其實數字不一定要按照順序填入，只要是連續數字皆可，更進一步，所填入的數字彼此間的差距為定值皆可滿足所求。		王顗嫣2025/8/25 下午 03:29:31

序號封面照內容說明上傳者最後修改
6類別 相簿集
名稱 討論魔方陣在生活中的應用
說明
8月27日組員們利用空閒時間討論魔方陣在生活中的應用以及延伸，在上網查詢資料後大家提出了不同想法，最後決定利用數獨來作為延伸的內容，以及組員也有查詢到一幅畫也是利用魔方正的概念在設計的。雖然數獨的規則和魔方陣並不一樣，但卻與模方陣有著類似的觀念，最後都需要是每一行每一列結果都一樣。那上述提到的那幅畫也展示出魔方陣在很久以前就出現了。		張羽涵2025/8/27 上午 10:38:21
5類別 相簿集
名稱 蒐集研究資料
說明
小組成員各自分工合作，透過網路資源深入查詢與研究主題相關的資訊；同時將蒐集到的內容進行整理、歸納與記錄，確保後續研究能夠有充足且有系統的資料做支撐。		劉宥陞2025/8/27 上午 08:49:14
4類別 相簿集
名稱 討論內容及修改
說明
8/25日，我們上線討論報告書的內容應該要新增那些文字及圖片，使此份報告內容更豐富。
經過昨天的討論過後，我們決定在目的的地方加上一點:「魔術方陣在生活中的應用」
因為此研究是從我們生活中發想出來的主題，所以回到生活中，想去尋找概念上與魔術方陣相似的應用。這些發想會從各自的生活中出發，再到網路上查詢、實證其概念與規則。		王顗嫣2025/8/26 上午 11:10:51
3類別 相簿集
名稱 討論研究方法
說明
組員們利用空間討論研究方法，先討論了各種可能的做法，並思考哪一種最符合我們的主題與需要。經過大家一起討論後，大家找出了最合適的方法來進行研究。在確定方法的同時，我們也規劃了接下來的流程，包括如何收集資料、如何分工合作，以及完成的時間安排。透過這樣的規劃，可以讓研究更有條理，也能確保每位組員清楚自己的任務，讓整個研究能夠順利推進。		張羽涵2025/8/25 下午 02:10:37
2類別 相簿集
名稱 參考歷屆做品
說明
05/17，在學校專題課時，運用時間一起上網參考歷屆的數學作品，並進行主題發想。
一開始想到個五、六個可能可行的方向後，上網搜尋是否已有相似的作品。經過小組和指導老師討論後，我們最後選擇魔術方陣這個主題進行本次的研究探討，我們往幾個比較有興趣的目的前進，像是歷史的探討、排列組合、生活中應用...等等。		王顗嫣2025/8/25 上午 11:51:33
1類別 相簿集
名稱 線上討論
說明
我們透過線上討論和組員們釐清方向，讓我們確定了主題和目標。		趙向2025/8/23 下午 02:32:14

序號內容上傳者最後修改
5作者 劉宥陞
標題 尋找一本書
內容
《數學魔方陣》由李國賢老師撰寫，系統介紹了魔方陣的起源、數學原理及建構方法，從奇數階、偶數階到特殊排列一應俱全，並結合趣味與應用，讓數字遊戲變得既有邏輯挑戰，也充滿藝術感。閱讀這本書時，就像跟著一位耐心的老師探索數字的世界，每完成一個魔方陣，就好似拼好了一幅精美的拼圖，既增強數學推理能力，也讓人感受到數學的秩序與美感。

劉宥陞2025/8/31 下午 09:10:05
4作者 王顗嫣
標題 討論報告內容
內容
在8/27大家線上討論修訂報告書的內容，今天大家一起討論魔術方陣在生活中的應用。
每個人都有很多很棒的點子，大家也都願意提出各自不同的想法，讓今天的討論順利進行，也很快地就打完了報告書的內文。
在這次小論文中我的收穫良多，不僅了解數學的許多歷史，也更懂得在討論意見不合的狀況下，與組員溝通及商量，讓小組內達到共識，而不是無止盡的爭吵。

王顗嫣2025/8/27 上午 10:27:16
3作者 張羽涵
標題 研究內容討論
內容
在5/24的專題課中原本組員們在討論本次研究的主題及方向，而在過程中有一位同學偶然間提出在金庸小說中有提到一個和魔術方陣相關的題目，立刻引起了我們濃厚的興趣與好奇心，於是我們便決定往這個方向展開研究。
討論過後，大家決定先從魔術方陣的歷史、種類以及背景開始了解，在簡單的查詢資料後，大家對於這個主題也有了基礎的認識，我們也希望未在來能從不同面向，嘗試延伸出更多元的研究方向，讓專題內容更為完整且具有深度。。

張羽涵2025/8/25 下午 02:19:55
2作者 王顗嫣
標題 訂出研究目的
內容
在6/21日的數學專題課程中，我們先進行文獻的探討，上網搜尋了許多資料。訂出了四項的研究目的，包括魔術方陣的規則、種類、歷史發展及在生活中的應用。
在這些目的中，最吸引我們往下探討的是魔術方陣中的「規則」，因為在不同種類的魔術方陣中的規則中有許多不同的限制，例如:每次往右上移動等。這讓我們想要往下探討如果我們往其他方向進行移動，此魔術方陣是否能成立。

王顗嫣2025/8/25 下午 12:16:40
1作者 趙向
標題 魔術方陣的規則
內容
我們在查詢資料時，我發現居然有這麼多種魔方陣，而其規則、限制盡皆不同，這令我對魔方陣更加好奇，並統整出六個常見的魔術方陣，它們的規則及限制，以及這些魔方陣的方法。

趙向2025/8/22 下午 02:36:43

序號封面簡介（摘要）上傳者最後修改
4書名 新版 魔方陣の世界
作者 大森清美
出版社 日本評論社
簡介（摘要）
這是Magkatsu 系列的完整介紹，涵蓋了從歷史到數學理論的廣泛主題。除了更細緻的講解之外，我們還添加了數百個魔術隊的實際例子。
導讀
這本全面更新的幻方陣入門書籍涵蓋了從歷史到數學理論的廣泛主題。它提供了更詳細的解釋，並包含數百個額外的幻方陣範例		趙向2025/9/13 上午 08:41:33
3書名 《數學魔方陣》
作者 李國賢
出版社 益智工房
簡介（摘要）
《數學魔方陣》介紹魔方陣的定義、歷史與發展，詳細講解奇數階與偶數階魔方陣的建構方法，並收錄各種特殊類型與應用，內容兼具系統性與趣味性，適合對數學邏輯、數字排列和結構設計有興趣的讀者作為入門與進階參考。
導讀
《數學魔方陣》是一部結合數學原理與趣味遊戲的書籍，透過系統化的講解帶領讀者了解魔方陣的起源、歷史、基本概念以及各種建構方法。書中從奇數階、偶數階到特殊排列，都有詳盡的步驟與示例，既適合數學初學者入門，也能滿足進階讀者對結構與規律的探索欲望。閱讀這本書，你不只是學會排列數字，更能感受到數學中的秩序、對稱與美感，並激發邏輯思維與解題能力。		劉宥陞2025/8/31 下午 09:16:18
2書名 有趣的數學魔方陣
作者 談祥伯
出版社 豐閣文化出版社
簡介（摘要）
書中首先從中國古代的「洛書」談起，介紹魔方陣的起源與歷史發展，帶領讀者走訪中國、印度、阿拉伯與歐洲文化中魔方陣的足跡。接著，作者系統性地說明各種不同階數的魔方陣，從最基本的三階到高階建構方式，包括奇數階的「斜對角法」、雙偶數階的「四象限交換法」，以及六階、八階的排列技巧。書中也延伸介紹了幻圓、幻星、魔術立方體等立體或特殊圖形的變化形式，讓魔方陣跳脫平面，展現更多數學之美。

導讀
這本書的重點圍繞在「魔方陣」的歷史、分類與建構方法。作者從最早的中國洛書談起，一路介紹了印度、伊斯蘭世界、歐洲等地的魔方陣發展，讓我們可以看到不同文化對於這種數字排列的理解與應用。不只是歷史背景豐富，書中也清楚地分類出各種階數魔方陣的製作方式，例如奇數階的斜對角法、偶數階的分區交換法等等，都有步驟說明與範例，非常容易理解。		張羽涵2025/8/26 下午 07:54:22
1書名 魔術方陣－動腦的數字遊戲
作者 蘇勝宏
出版社 德威國際文化事業有限公司
簡介（摘要）
這本書《魔數方陣》是作者根據中國古代的洛書九宮算演變而來的魔術方陣。在「魔數方陣」書中，教了許多技巧如何解出魔術方陣，例如:可以先從最簡單、最小的方陣開始如單數魔方陣(3X3九宮格）以進信心，再逐漸到困難度高的、大的方陣。依自己的程度慢慢提升困難度，以挑戰自己的能力......等等。
導讀
「魔數方陣」在解題時最重要的是的解題技巧是從行、列中空格最少的先開始。它是正方形的數列，又每一行、每一列的「和」都相等，且每一個數字在整個方陣數列中只能出現一次，不可重複，所以可以把空格逐漸把空格填滿。書裡也有從最簡單的3X3九宮格，逐漸到比較困難的5X5二十五格、7X7四十九格......甚至是(2n+1)2到無窮大的正方形數列陣，等著我們去挑戰!		王顗嫣2025/8/25 下午 03:18:08

序號截圖網站簡介上傳者最後修改
5網站名稱 4N 魔方陣
網址 https://openhome.cc/zh-tw/algorithm/matrix/evenly-even-magic/
網站簡介
《4N 魔方陣》介紹了一種雙偶數（階數為 4 的倍數）的魔方陣，其特點是每一行、每一列和兩條對角線的數字總和都相等。構建方法是將方陣分為對角線區域和非對角線區域，先順序填入非對角線位置，再逆序填入對角線位置，透過這種補充方式，最終形成完整且符合魔方陣條件的排列。
劉宥陞2025/8/31 下午 09:20:28
4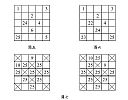網站名稱 騎士漫遊方陣與魔方陣
網址 https://www.math.sinica.edu.tw/media/pdf/d283/28308.pdf
網站簡介
這篇網站主要是在講述魔術方陣是一種在兩千多年前就出現的數字方陣，而它每一行每一列以及每個對角線的合都相等，而騎士漫遊方陣是西方人發現的數字方陣。 最早研究的人是瑞士數學天才歐拉, 他在1759年 發表他的結果，在經過後續的研究後發現三階和四階的騎士漫遊方陣都是不存在的。
張羽涵2025/8/25 下午 02:32:11
3網站名稱 魔方陣
網址 http://www.mathland.idv.tw/fun/mag.htm
網站簡介
網站中簡介了魔術方陣的歷史，從金庸小說的射雕英雄傳的一個題目「九宮之義，法以靈龜，二四為肩，六八為足，左三右七，戴九履一，五居中央」進行介紹魔術方的特性及每個橫﹐列﹐對角線之間的關聯。
王顗嫣2025/8/25 上午 11:38:36
2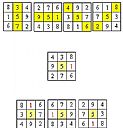網站名稱 卜個卦嗎？---- 河圖、洛書、魔方陣
網址 https://calculus.math.nycu.edu.tw/maple/Site/carnival/magic/203.htm
網站簡介
把數字1, 2, …n平方，填入n平方個小正方形組成的正方形方陣裡，使得縱、橫、對角線的和都相同。這樣一個神奇的方陣就稱為“魔方陣”。 		趙向2025/8/23 下午 05:56:11
1網站名稱 123 看誰先達陣
網址 https://serc.tn.edu.tw/wp-content/uploads/2020/06/ES18_%E9%AD%94%E6%96%B9%E9%99%A3123%E7%9C%8B%E8%AA%B0%E5%85%88%E9%81%94%E9%99%A3.pdf
網站簡介
在透過簡潔連續法的解法中發現，只要 N 為奇數，且 N>3，N 階魔方陣就能透過簡潔連續法找出 N 種解法。		趙向2025/8/23 下午 05:55:38

序號書面報告說明上傳者最後修改
1說明 藏在方格裡的智慧：魔術方陣的歷史與規則
書面報告		趙向2025/9/26 下午 10:57:53